Aparentemente, dinâmica estelar soa como um problema extremamente simples. O sistema físico é muito bem definido, uma coleção de partículas, e a única física envolvida é a Mecânica Clássica com a Gravitação Newtoniana. Tudo o que é preciso fazer é definir o estado inicial do sistema e integrar as equações de movimento para determinar o estado do sistema em qualquer momento futuro. A cilada, no entanto, encontra-se, evidentemente, no fato de que o cálculo das equações é impraticável quando o número de partículas é suficientemente grande para representar um sistema real. As saídas para esta dificuldade são duas, tratar estatisticamente o sistema, o que é basicamente feito nas simulações, ou buscar soluções analíticas aproximadas e particulares.
É possível atualmente realizar simulações numéricas sem se conhecer de fato toda a física e matemática que se encontra por trás dos códigos e pacotes de programas disponíveis em nível mundial. Entretanto, é evidentemente de suma importância conhecer de maneira detalhada o problema que se quer resolver com as simulações. Assim, nesta seção, apresentamos a essência do que já se foi realizado em dinâmica estelar e é para nós relevante, incluindo também uma motivação para as simulações.
Considere um conjunto muito grande de estrelas que se movem sob a influência de um potencial
![]() . Em qualquer instante de tempo
. Em qualquer instante de tempo ![]() , é possível dar uma descrição completa do
sistema, especificando o número de estrelas
, é possível dar uma descrição completa do
sistema, especificando o número de estrelas
![]() cujas posições se encontram num volume infinitesimal
cujas posições se encontram num volume infinitesimal
![]() e cujas velocidades se
encontram num volume infinitesimal
e cujas velocidades se
encontram num volume infinitesimal
![]() . A função
. A função
![]() é
chamada de função de distribuição ou densidade no espaço de fase do sistema.
é
chamada de função de distribuição ou densidade no espaço de fase do sistema.
Podemos portanto definir as coordenadas no espaço de fase como
![]() . A velocidade com que as estrelas
se movimentam no espaço de fase pode ser entendida então como
. A velocidade com que as estrelas
se movimentam no espaço de fase pode ser entendida então como
![]() 13. Se desconsiderarmos encontros
entre as estrelas, i.e., se o movimento de cada estrela puder ser considerado como aquele
provocado pelo potencial médio de todo o sistema, então as estrelas fluirão continuamente no
espaço de fase e, portanto,
13. Se desconsiderarmos encontros
entre as estrelas, i.e., se o movimento de cada estrela puder ser considerado como aquele
provocado pelo potencial médio de todo o sistema, então as estrelas fluirão continuamente no
espaço de fase e, portanto, ![]() deve satisfazer à equação de continuidade:
deve satisfazer à equação de continuidade:
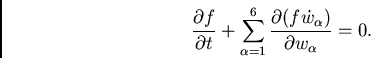 |
(30) |
Podemos interpretar o sentido físico da Eq. (3.2) se a integrarmos em um dado volume no espaço
de fase. Daí, teremos que o primeiro termo descreve a taxa com que o conteúdo estelar dentro
deste volume varia no tempo. O segundo termo, utilizando o teorema da divergência (ou teorema de
Gauss, ver BT87), descreve a taxa com que estrelas fluem através da superfície matemática que envolve
este volume. Evidentemente, com a convenção correta de sinais a soma destes termos deve se
anular. Esta equação de continuidade é análoga à de um fluxo de um fluido ordinário.
Já que ![]() e
e ![]() são coordenadas independentes do espaço de
fase, e
são coordenadas independentes do espaço de
fase, e
![]() também não depende de
também não depende de ![]() , então:
, então:
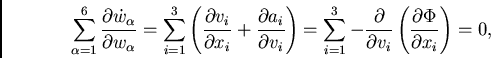 |
(31) |
onde
![]() e
e
![]() .
.
A Eq. (3.3) nos permite simplificar a Eq. (3.2). Assim,
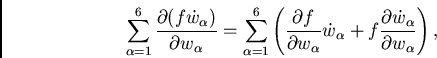 |
(32) |
mas o segundo termo entre parênteses na Eq. (3.4) é nulo e, portanto, temos:
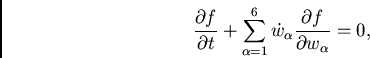 |
(33) |
ou ainda,
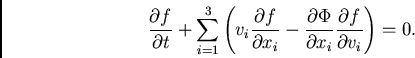 |
(34) |
Em notação vetorial, temos:
| (35) |
Esta última é a equação acolisional de Boltzmann, também conhecida como a
equação de Vlasov, e é, evidentemente, uma equação fundamental da dinâmica estelar. Note
que, se considerarmos encontros entre as estrelas, a força ![]() não será apenas resultado
do potencial médio do sistema, de forma que
não será apenas resultado
do potencial médio do sistema, de forma que
![]() depende de
depende de ![]() durante as
colisões (isso será explicitado adiante). Sendo assim, as colisões invalidam a Eq. (3.3). O efeito
de colisões é o de introduzir um termo à direita na Eq. (3.7), o que também veremos adiante.
durante as
colisões (isso será explicitado adiante). Sendo assim, as colisões invalidam a Eq. (3.3). O efeito
de colisões é o de introduzir um termo à direita na Eq. (3.7), o que também veremos adiante.
Vamos mostrar agora que a equação acolisional de Boltzmann é um caso especial de uma equação
ainda mais fundamental, que é a equação de Liouville. Analogamente à argumentação que
realizamos com a função de distribuição no espaço de fase, podemos utilizar a formulação de
Gibbs, imaginando um espaço com ![]() dimensões, chamado espaço-
dimensões, chamado espaço-![]() . As
coordenadas neste espaço são as coordenadas do espaço de fase de todas as estrelas. Assim,
um ponto no espaço-
. As
coordenadas neste espaço são as coordenadas do espaço de fase de todas as estrelas. Assim,
um ponto no espaço-![]() representa o estado completo de um sistema de
representa o estado completo de um sistema de ![]() estrelas em
um dado instante de tempo
estrelas em
um dado instante de tempo ![]() . Este ponto-
. Este ponto-![]() é portanto determinado pela coleção
de
é portanto determinado pela coleção
de ![]() vetores de 6 dimensões,
vetores de 6 dimensões,
![]() . A evolução
do sistema segue uma curva no espaço-
. A evolução
do sistema segue uma curva no espaço-![]() .
.
A probabilidade de que o dado sistema se encontre numa configuração específica é, portanto,
a probabilidade de que um ponto-![]() seja encontrado num certo volume no
espaço-
seja encontrado num certo volume no
espaço-![]() em um determinado instante; i.e.,
em um determinado instante; i.e.,
![]() .
A condição de normalização é:
.
A condição de normalização é:
| (36) |
onde
![]() . A função
. A função ![]() é conhecida como a função de distribuição de
é conhecida como a função de distribuição de ![]() -partículas. A dedução da equação que
governa a evolução de
-partículas. A dedução da equação que
governa a evolução de ![]() é exatamente análoga à dedução da equação acolisional de
Boltzmann, que governa a evolução da densidade no espaço de fase, ou função de
distribuição,
é exatamente análoga à dedução da equação acolisional de
Boltzmann, que governa a evolução da densidade no espaço de fase, ou função de
distribuição, ![]() (ver, e.g., BT87).
(ver, e.g., BT87).
Assim, pode-se chegar, finalmente, à equação de Liouville:
![\begin{displaymath}
\frac{\partial f^{(N)}}{\partial t} + \sum_{\alpha=1}^{N} \l...
...dot
\frac{\partial f^{(N)}}{\partial \vec{v}_\alpha}\right]=0,
\end{displaymath}](img290.png) |
(37) |
onde ![]() é o potencial na estrela
é o potencial na estrela ![]() devido a todas as outras
devido a todas as outras ![]() estrelas.
estrelas.
Vamos agora definir a função de distribuição de 1-partícula:
| (38) |
Se integrarmos agora a equação de Liouville sobre todas as estrelas, exceto uma, i.e.,
se integrarmos sobre
![]() , o termo que envolve
, o termo que envolve
![]() nos dá
nos dá
![]() . Os termos que envolvem
. Os termos que envolvem
![]() e
e
![]() se
anulam quando
se
anulam quando
![]() , e, portanto, obtemos:
, e, portanto, obtemos:
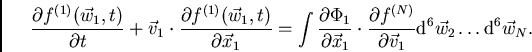 |
(39) |
O potencial na estrela ![]() é
é
![]() , onde
, onde
![]() . Para simplificar, consideremos
que todas as estrelas são iguais, i.e., têm a mesma massa. Daí,
podemos escrever o lado direito da Eq. (3.11) como:
. Para simplificar, consideremos
que todas as estrelas são iguais, i.e., têm a mesma massa. Daí,
podemos escrever o lado direito da Eq. (3.11) como:
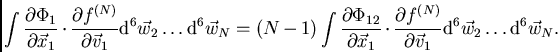 |
(40) |
Agora, se definirmos a função de distribuição de 2-partículas como:
| (41) |
então obtemos:
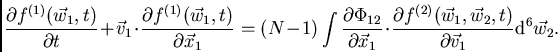 |
(42) |
A Eq. (3.14) descreve a variação temporal de
![]() em termos de
em termos de
![]() . Uma equação similar pode ser obtida para
. Uma equação similar pode ser obtida para
![]() em termos de
em termos de
![]() .
Assim, podemos obter uma seqüência de equações conhecida como a
hierarquia BBGKY (Bogoliubov, Born, Green, Kirkwood e Yvon descobriram as equações
independentemente entre 1935 e 1946). Determinar uma solução exata para a hierarquia
não é mais fácil do que obter uma para a própria equação de Liouville, já que
a solução para
.
Assim, podemos obter uma seqüência de equações conhecida como a
hierarquia BBGKY (Bogoliubov, Born, Green, Kirkwood e Yvon descobriram as equações
independentemente entre 1935 e 1946). Determinar uma solução exata para a hierarquia
não é mais fácil do que obter uma para a própria equação de Liouville, já que
a solução para ![]() precisa ser conhecida antes de se determinar
precisa ser conhecida antes de se determinar ![]() . Entretanto, a
hierarquia BBGKY pode ser fechada, utilizando-se aproximações adequadas.
. Entretanto, a
hierarquia BBGKY pode ser fechada, utilizando-se aproximações adequadas.
Podemos escrever ![]() como:
como:
| (43) |
onde ![]() é a chamada função de correlação de 2-partículas, pois, grosso
modo,
é a chamada função de correlação de 2-partículas, pois, grosso
modo, ![]() expressa o excesso de probabilidade de se encontrar uma partícula
em
expressa o excesso de probabilidade de se encontrar uma partícula
em ![]() devido
à presença de outra partícula em
devido
à presença de outra partícula em ![]() , e vice-versa.
, e vice-versa.
Podemos também verificar que há uma estreita relação entre a função de distribuição
![]() e a função de distribuição de 1-partícula
e a função de distribuição de 1-partícula
![]() . De fato,
. De fato,
![]() e
e
![]() , e, portanto,
, e, portanto, ![]() .
Assim, podemos substituir na Eq. (3.14)
.
Assim, podemos substituir na Eq. (3.14)
![]() por
por
![]() . Além
disso, também podemos substituir, no último termo da Eq. (3.14), a Eq. (3.15) para
. Além
disso, também podemos substituir, no último termo da Eq. (3.14), a Eq. (3.15) para
![]() . Então, teremos que:
. Então, teremos que:
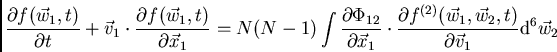 |
(44) |
![\begin{displaymath}
=N(N-1)\int \frac{\partial\Phi_{12}}{\partial\vec{x}_1} \cdo...
...}_2,t)}{N^2}+g(\vec{w}_1,\vec{w}_2,t)\right]{\rm d}^6\vec{w}_2
\end{displaymath}](img320.png) |
(45) |
![\begin{displaymath}
=N(N-1) \int \frac{\partial\Phi_{12}}{\partial\vec{x}_1} \cd...
...}_1,\vec{w}_2,t)}{\partial\vec{v}_1}\right]{\rm d}^6\vec{w}_2,
\end{displaymath}](img321.png) |
(46) |
mas como
![]() , continuamos com:
, continuamos com:
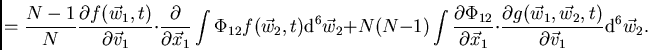 |
(47) |
Agora, supondo que ![]() , de modo que
, de modo que ![]() , e notando que:
, e notando que:
| (48) |
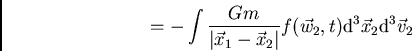 |
(49) |
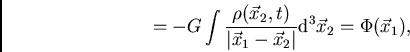 |
(50) |
onde ![]() e
e ![]() são, respectivamente, a densidade total e o
potencial total em
são, respectivamente, a densidade total e o
potencial total em ![]() devido a todo o sistema, finalmente, então, obtemos:
devido a todo o sistema, finalmente, então, obtemos:
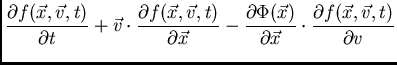 |
|||
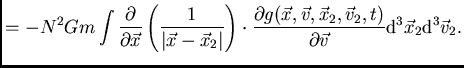 |
(51) |
Para termos chegado a esta equação, simplesmente partimos da equação de Liouville e fizemos
2 hipóteses bastante razoáveis, i.e., um número grande de estrelas no sistema, e todas as
estrelas com mesma massa (essa última não tão razoável!). No entanto, não podemos
resolvê-la, pois não conhecemos a função de correlação
![]() ! Podemos, é claro, escolher uma forma aproximada para
essa função, e, a mais simples possível é
! Podemos, é claro, escolher uma forma aproximada para
essa função, e, a mais simples possível é ![]() . Ao fazer esta escolha, estamos ignorando
colisões entre as estrelas, e justamente a Eq. (3.23) torna-se, então, a equação acolisonal de
Boltzmann.
. Ao fazer esta escolha, estamos ignorando
colisões entre as estrelas, e justamente a Eq. (3.23) torna-se, então, a equação acolisonal de
Boltzmann.
Vejamos agora qual é o efeito das colisões14 entre estrelas de um dado sistema. Podemos obter uma estimativa grosseira, porém instrutiva, com as seguintes aproximações: (i) a estrela perturbadora permanece estacionária, (ii) o movimento da estrela pertubada segue retilíneo, e (iii) somente a componente da força perpendicular ao movimento da estrela é importante. Imagine duas estrelas colidindo segundo a geometria apresentada na Fig. 3.1. A força resultante da colisão sobre cada estrela pode ser expressa como:
![\begin{displaymath}
F_\perp = \frac{Gm^2}{b^2+x^2}{\rm cos}\theta = \frac{Gm^2b}...
...c{Gm^2}{b^2}\left[1+\left(\frac{vt}{b}\right)^2\right]^{-3/2},
\end{displaymath}](img336.png) |
(52) |
já que podemos aproximar ![]() por
por ![]() .15 Queremos determinar qual é a variação
na velocidade da estrela devido à colisão. Temos que:
.15 Queremos determinar qual é a variação
na velocidade da estrela devido à colisão. Temos que:
![\begin{displaymath}
\dot{v}_\perp = \frac{Gm}{b^2}\left[1+\left(\frac{vt}{b}\rig...
...b^2}\left[1+\left(\frac{vt}{b}\right)^2\right]^{-3/2}{\rm d}t.
\end{displaymath}](img339.png) |
(53) |
Fazendo a substituição de variáveis ![]() , obtemos:
, obtemos:
| (54) |
Vemos que a variação da velocidade devido à colisão é aproximadamente o produto
da aceleração sofrida durante a aproximação máxima (![]() ) e um intervalo de tempo
(
) e um intervalo de tempo
(![]() ), que pode ser definido como a duração do encontro. Note que consideramos que o
movimento da estrela mesmo durante a colisão é retilíneo e uniforme, i.e., o movimento da
estrela pouco se altera. Assim, essa análise só é válida para
), que pode ser definido como a duração do encontro. Note que consideramos que o
movimento da estrela mesmo durante a colisão é retilíneo e uniforme, i.e., o movimento da
estrela pouco se altera. Assim, essa análise só é válida para
![]() .
Dentro deste limite temos então o que é chamado de aproximação impulsiva.
.
Dentro deste limite temos então o que é chamado de aproximação impulsiva.
Como no caso do movimento browniano, os encontros são aleatórios, e o valor médio da
variação da velocidade da estrela, ![]() , é nulo. No entanto, o valor
acumulado de
, é nulo. No entanto, o valor
acumulado de ![]() aumenta a cada encontro. Assim sendo, após um número suficientemente grande de encontros,
o movimento da estrela foi alterado de tal forma que desconsiderar colisões acaba sendo
uma aproximação não justificada.
aumenta a cada encontro. Assim sendo, após um número suficientemente grande de encontros,
o movimento da estrela foi alterado de tal forma que desconsiderar colisões acaba sendo
uma aproximação não justificada.
Em Mecânica Estatística, sabemos que as colisões entre as partículas em um gás ordinário induz uma troca de energia entre as partículas, o que vai levando o sistema a uma situação de equipartição de energia. É o que faz com que dois corpos a diferentes temperaturas atinjam uma temperatura de equilíbrio após terem sido colocados em contato por um tempo suficientemente longo. O tempo que o sistema leva para atingir o estado de equilíbrio é chamado de tempo de relaxação.
Voltando ao nosso sistema estelar, isolado, ligado gravitacionalmente, podemos definir o tempo de relaxação como sendo aquele em que a variação cumulativa da velocidade da estrela após muitos encontros é da ordem de grandeza da própria velocidade da estrela. Se um sistema estelar pode alcançar este estado num intervalo de tempo menor do que aquele em que a dinâmica do tal sistema será investigada, então a equação acolisional de Boltzmann não é mais válida; o efeito das colisões tem de ser levado em consideração.
Considerando que o número de colisões envolvendo 2 corpos é certamente maior do que o número de colisões que envolvem um número maior de estrelas, então podemos determinar qual é o tempo de relaxação de um sistema estelar utilizando o formalismo iniciado na Eq. (3.24). Teremos então o tempo de relaxação a dois corpos.
Podemos estimar o número de colisões ![]() sofridas por uma estrela, ao cruzar um sistema,
como sendo o produto da seção de choque da colisão, correspondente a um parâmetro de
impacto entre
sofridas por uma estrela, ao cruzar um sistema,
como sendo o produto da seção de choque da colisão, correspondente a um parâmetro de
impacto entre ![]() e
e ![]() , com a densidade superficial do sistema. Assim, temos:
, com a densidade superficial do sistema. Assim, temos:
| (55) |
![]() é o raio característico do sistema. A variação quadrática da velocidade será
então:
é o raio característico do sistema. A variação quadrática da velocidade será
então:
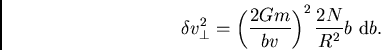 |
(56) |
Devemos calcular agora a variação total da velocidade
![]() ,
o que podemos fazer integrando a
equação acima sobre todos os parâmetros de impacto possíveis. Felizmente, não há sentido
físico em considerarmos
,
o que podemos fazer integrando a
equação acima sobre todos os parâmetros de impacto possíveis. Felizmente, não há sentido
físico em considerarmos ![]() , e nem
, e nem
![]() , pois a integral diverge em
ambos os casos. Devemos limitar
, pois a integral diverge em
ambos os casos. Devemos limitar ![]() , então. Como limite superior, é natural considerarmos
, então. Como limite superior, é natural considerarmos ![]() ,
o tamanho característico do sistema. Por outro lado, uma escolha natural para o limite inferior
é aquele em que saímos do limite de aproximação impulsiva. Ou seja,
,
o tamanho característico do sistema. Por outro lado, uma escolha natural para o limite inferior
é aquele em que saímos do limite de aproximação impulsiva. Ou seja,
![]() . Então,
temos:
. Então,
temos:
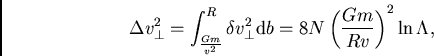 |
(57) |
onde
![]() é o chamado logaritmo de Coulomb. Este
termo surge também no tratamento de espalhamento em plasmas.
é o chamado logaritmo de Coulomb. Este
termo surge também no tratamento de espalhamento em plasmas.
Assumindo velocidades Keplerianas (![]() ), como
), como ![]() é a massa total do sistema,
então:
é a massa total do sistema,
então:
| (58) |
Se a cada vez que uma estrela percorre o sistema sua velocidade se altera devido às colisões
por um valor
![]() , o número de vezes que a estrela deve atravessar o sistema
para que
, o número de vezes que a estrela deve atravessar o sistema
para que
![]() é dado por
é dado por
![]() . E o tempo
de relaxação do sistema é, portanto,
. E o tempo
de relaxação do sistema é, portanto,
![]() , onde
, onde ![]() é o tempo de
cruzamento do sistema. Então:
é o tempo de
cruzamento do sistema. Então:
| (59) |
Usando as relações acima para ![]() ,
, ![]() e
e ![]() , então
, então ![]() , e, assim:
, e, assim:
| (60) |
A equação acima nos diz que uma estrela se desvia sensivelmente
de sua trajetória original (aquela induzida
apenas pelo potencial médio do sistema), devido ao efeito cumulativo de colisões, apenas após
cerca de ![]() vezes o tempo de cruzamento do sistema. Portanto, mesmo para um sistema
pequeno, com cerca de 100 estrelas por exemplo, o efeito das colisões só é perceptível
após a estrela ter cruzado o sistema pelo menos algumas vezes. Para estes pequenos sistemas, o
tratamento acolisional é justificável se a evolução do sistema for acompanhada por um tempo que
não seja demasiado longo. Vejamos alguns exemplos. Um aglomerado estelar aberto possui cerca
de 100 estrelas, e um tempo de cruzamento característico da ordem de
vezes o tempo de cruzamento do sistema. Portanto, mesmo para um sistema
pequeno, com cerca de 100 estrelas por exemplo, o efeito das colisões só é perceptível
após a estrela ter cruzado o sistema pelo menos algumas vezes. Para estes pequenos sistemas, o
tratamento acolisional é justificável se a evolução do sistema for acompanhada por um tempo que
não seja demasiado longo. Vejamos alguns exemplos. Um aglomerado estelar aberto possui cerca
de 100 estrelas, e um tempo de cruzamento característico da ordem de ![]() anos. Estes
sistemas são tipicamente jovens, com idades da ordem de
anos. Estes
sistemas são tipicamente jovens, com idades da ordem de ![]() anos. Assim, a evolução
completa de um aglomerado aberto só pode ser devidamente acompanhada com técnicas que
incluam colisões. O mesmo ocorre para aglomerados globulares
(
anos. Assim, a evolução
completa de um aglomerado aberto só pode ser devidamente acompanhada com técnicas que
incluam colisões. O mesmo ocorre para aglomerados globulares
(
![]() anos, idade
anos, idade
![]() anos), o núcleo de um
aglomerado globular, onde
anos), o núcleo de um
aglomerado globular, onde ![]() é curto, e o núcleo de galáxias
(
é curto, e o núcleo de galáxias
(
![]() anos, idade
anos, idade
![]() anos). Para aglomerados
de galáxias (
anos). Para aglomerados
de galáxias (
![]() anos, idade
anos, idade
![]() anos) a
importância das colisões pode depender da estrutura do aglomerado.
anos) a
importância das colisões pode depender da estrutura do aglomerado.
De qualquer forma, mesmo para sistemas em que a análise do tempo de relaxação indica que colisões são importantes, alguns autores não as consideram, argumentando que a evolução dinâmica do sistema é essencialmente aquela de um sistema acolisional. Certamente isto é verdade, especialmente se o tempo considerado for curto.
Para galáxias, entretanto,
![]() ,
,
![]() anos e a idade
anos e a idade
![]() anos, de forma que encontros estelares não são importantes
para a evolução dinâmica de galáxias.
anos, de forma que encontros estelares não são importantes
para a evolução dinâmica de galáxias.
Vimos que os encontros estelares fazem com que o movimento das estrelas não seja unicamente
determinado pelo potencial médio do sistema e, sendo assim,
![]() passa a depender
de
passa a depender
de ![]() durante as colisões. Assim, a suposição contrária, que foi utilizada na dedução da
equação acolisional de Boltzmann, passa a ser inválida. Portanto, matematicamente, o efeito
das colisões é o de introduzir um termo à direita na equação:
durante as colisões. Assim, a suposição contrária, que foi utilizada na dedução da
equação acolisional de Boltzmann, passa a ser inválida. Portanto, matematicamente, o efeito
das colisões é o de introduzir um termo à direita na equação:
| (61) |
onde ![]() é o termo colisional que nos dá a taxa de variação da função de
distribuição devido a encontros. Consideremos
é o termo colisional que nos dá a taxa de variação da função de
distribuição devido a encontros. Consideremos
![]() a
probabilidade de que uma estrela com as coordenadas no espaço de fase
a
probabilidade de que uma estrela com as coordenadas no espaço de fase ![]() seja
deslocada (devido aos encontros) para um outro volume no espaço de fase
seja
deslocada (devido aos encontros) para um outro volume no espaço de fase
![]() em torno de
em torno de
![]() no intervalo de tempo
no intervalo de tempo ![]() . Então, as estrelas que
são expulsas de um certo volume unitário no espaço de fase centrado em
. Então, as estrelas que
são expulsas de um certo volume unitário no espaço de fase centrado em ![]() o fazem
com a seguinte taxa:
o fazem
com a seguinte taxa:
| (62) |
Por outro lado, os encontros que põem estrelas dentro deste volume acontecem com a taxa de:
| (63) |
Assim, o termo colisional é:
| (64) |
| (65) |
Esta equação foi obtida integrando a Eq. (3.29) sobre todos os parâmetros de impacto
justificáveis fisicamente. Se quisermos saber a contribuição para
![]() das colisões
que ocorrem com parâmetros de impacto entre
das colisões
que ocorrem com parâmetros de impacto entre ![]() e
e ![]() , basta substituírmos
, basta substituírmos
![]() por
por ![]() . Isso significa que para intervalos logarítmicos de
. Isso significa que para intervalos logarítmicos de ![]() iguais, a
contribuição para
iguais, a
contribuição para
![]() é igual, o que nos permite dizer que são os encontros com
parâmetros de impacto grandes os que mais contribuem para o processo de
relaxação.16Como estes encontros produzem variações pequenas na velocidade, então as variações
no espaço de fase também são pequenas, i.e.,
é igual, o que nos permite dizer que são os encontros com
parâmetros de impacto grandes os que mais contribuem para o processo de
relaxação.16Como estes encontros produzem variações pequenas na velocidade, então as variações
no espaço de fase também são pequenas, i.e.,
![]() é pequeno. Então
podemos expandir o primeiro termo no termo colisional em séries de Taylor:
é pequeno. Então
podemos expandir o primeiro termo no termo colisional em séries de Taylor:
![$\displaystyle -\sum_{i=1}^{6}\Delta w_i \frac{\partial}{\partial w_i}\left[\Psi(\vec{w},\Delta\vec{w})
f(\vec{w})\right]$](img401.png) |
(66) | ||
![$\displaystyle +\frac{1}{2}\sum_{i,j=1}^{6}\Delta w_i \Delta w_j
\frac{\partial^...
...\left[\Psi(\vec{w},\Delta\vec{w}) f(\vec{w})\right]
+ {\rm O}(\Delta\vec{v}^3).$](img402.png) |
Podemos aproximar a Eq. (3.38), truncando a série após os termos de segunda ordem:
![\begin{displaymath}
\Gamma(f) = -\sum_{i=1}^{6} \frac{\partial}{\partial w_i}\le...
...partial w_j}\left[
f(\vec{w}) D(\Delta w_i,\Delta w_j)\right],
\end{displaymath}](img403.png) |
(67) |
onde os coeficientes de difusão ![]() indicam a expectativa de variação em
indicam a expectativa de variação em
![]() por unidade de tempo:
por unidade de tempo:
| (68) |
com uma definição similar para
![]() .
.
A vantagem de utilizar os coeficientes de difusão é a de que todo o efeito das colisões na dinâmica do sistema está expresso por eles. Com essa análise, chegamos a uma equação que, portanto, envolve também os efeitos colisionais, e é mais geral que a equação de Boltzmann. Tal equação,
![\begin{displaymath}
\frac{\partial f}{\partial t} + \vec{v}\cdot\vec{\nabla} f -...
...partial w_j}\left[
f(\vec{w}) D(\Delta w_i,\Delta w_j)\right],
\end{displaymath}](img408.png) |
(69) |
é conhecida como a equação de Fokker-Planck. O primeiro passo na sua solução é encontrar os coeficientes de difusão. Duas aproximações apropriadas são utilizadas em geral. A primeira delas consiste em considerar os efeitos colisionais durante uma órbita da estrela pelo sistema, obtendo um efeito médio por órbita. A segunda aproximação é fundamentada na aproximação impulsiva (veja acima), o que implica em: (i) somente a velocidade da estrela sofre variação, não a sua posição; (ii) durante o encontro as estrelas movem-se em hipérboles Keplerianas, desconsiderando o potencial médio do sistema, e (iii) os efeitos são calculados como se a estrela estivesse inserida em um meio homogêneo infinito, no qual a função de distribuição é em todo lugar igual ao seu valor na posição da estrela.
A resolução da equação completa é similar à da equação de Boltzmann, desconsiderando, é claro, o termo colisional. Utilizando a equação de Poisson,
| (70) |
e considerando que a densidade no espaço ordinário pode ser obtida diretamente da função de distribuição, pois,
| (71) |
obtemos uma equação que descreve completamente a dinâmica do sistema (a integral é calculada sobre todas as velocidades):
| (72) |
A solução para ![]() , no entanto, é muito complexa. Para casos particulares, por exemplo, se
soubermos a densidade em função do raio para um sistema com simetria esférica e isotropia
na dispersão de velocidades, podemos obter
, no entanto, é muito complexa. Para casos particulares, por exemplo, se
soubermos a densidade em função do raio para um sistema com simetria esférica e isotropia
na dispersão de velocidades, podemos obter ![]() diretamente da Eq. (3.43). No entanto, além
de servir somente em casos particulares, as fórmulas assim obtidas para
diretamente da Eq. (3.43). No entanto, além
de servir somente em casos particulares, as fórmulas assim obtidas para ![]() (chamadas de
fórmulas de Eddington) não garantem que
(chamadas de
fórmulas de Eddington) não garantem que ![]() seja sempre maior do que zero, o que deve
ser verdade para qualquer sistema físico aceitável.
seja sempre maior do que zero, o que deve
ser verdade para qualquer sistema físico aceitável.
Através da equação de Boltzmann, também é possível obter informações físicas relevantes sobre o sistema considerado sem precisar resolver a equação. Isso se faz calculando os momentos da equação. O momento de ordem zero é obtido ao integrarmos a equação de Boltzmann sobre todas as velocidades, resultando em:
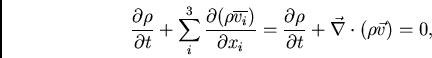 |
(73) |
que nada mais é que a equação de continuidade de massa do sistema
(
![]() é a velocidade média na componente
é a velocidade média na componente ![]() ).
).
O momento de segunda ordem é obtido multiplicando a equação de Boltzmann por uma
componente da velocidade, ![]() , e novamente integrando sobre todas as velocidades
possíveis, o que resulta em:
, e novamente integrando sobre todas as velocidades
possíveis, o que resulta em:
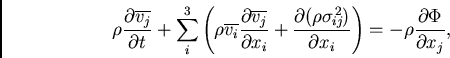 |
(74) |
onde ![]() é o tensor dispersão de velocidades, definido por:
é o tensor dispersão de velocidades, definido por:
| (75) |
Estas equações foram derivadas por Maxwell, mas foram utilizadas em astronomia pela primeira vez por James Jeans e, por isso, levam o nome de equações de Jeans. De qualquer forma, Maxwell já tem as suas famosas equações do eletromagnetismo!
Vimos, nesta longa seção, que o tratamento analítico do problema gravitacional de ![]() -corpos
em sistemas estelares é demasiado complexo. Não existem soluções exatas gerais para as
equações que nos permitem acompanhar a evolução dinâmica de um sistema; estas equações
somente nos dão a habilidade de inferir alguns resultados importantes e somente em casos
especiais. Soluções numéricas para a equação de Fokker-Planck só são possíveis
para sistemas esféricos.
-corpos
em sistemas estelares é demasiado complexo. Não existem soluções exatas gerais para as
equações que nos permitem acompanhar a evolução dinâmica de um sistema; estas equações
somente nos dão a habilidade de inferir alguns resultados importantes e somente em casos
especiais. Soluções numéricas para a equação de Fokker-Planck só são possíveis
para sistemas esféricos.
É interessante notar que, no entanto, apesar de o problema ser tão complexo analiticamente, e de parecer que o resultado de tantos esforços até hoje é pequeno, muitos resultados coerentes e importantes foram obtidos analiticamente. A formação de barras e braços espirais em discos de galáxias é um exemplo notável. Utilizando a equação de Boltzmann, a equação de Poisson, uma função apropriada para a densidade superficial, e ainda outras ferramentas matemáticas, nos foi possível prever as condições que fazem com que essas estruturas se desenvolvam (ver Seção 1.2). No entanto, não é possível analiticamente prever quando, durante a evolução dinâmica de um disco estelar, os braços espirais (ou a barra) se formam, ou qual a sua extensão, ou ainda como essas estruturas evoluem. Soluções analíticas são intratáveis no estudo de sistemas que se afastam do equilíbrio, como interações entre galáxias ou instabilidades dinâmicas, ou quando efeitos não lineares são importantes. É nesse ponto, finalmente, que entram as simulações numéricas! Com elas, é possível estimar, e.g., o tempo necessário para a formação de barras em discos, a extensão das barras e dos braços espirais, o efeito destas estruturas nas órbitas estelares, e até mesmo a evolução destas estruturas, em alguns casos, até sua completa dissolução. E estes são apenas alguns parcos exemplos.