



Next: 4 Resultados
Up: 3 Fotometria Superficial
Previous: 2 As imagens do
Contents
A distribuição de luz em galáxias pode ser estudada através de perfis radiais de
brilho superficial, em geral, em unidades de magnitudes por segundo de arco ao quadrado.
Estes podem ser decompostos, para galáxias espirais, em 2 componentes: uma que se refere ao bojo,
e outra correspondente ao disco. A função que mais se utiliza para descrever a componente disco do perfil de
brilho superficial de uma galáxia espiral é uma função exponencial, também conhecida como perfil de King
(ver Mihalas & Binney 1981). Esta função pode ser descrita como:
 |
(27) |
em luminosidade (erg 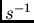 ). Ou como:
). Ou como:
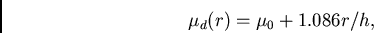 |
(28) |
em magnitudes. Nas equações acima, 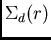 e
e 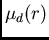 representam o brilho superficial do
disco em função da distância ao centro
representam o brilho superficial do
disco em função da distância ao centro 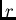 .
. 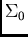 e
e 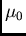 representam o brilho superficial central do
disco, e
representam o brilho superficial central do
disco, e 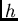 é o raio característico do disco.
Para a componente bojo, a função mais utilizada é aquela sugerida por de Vaucouleurs (ver Caon, Capaccioli &
D'Onofrio 1993 e referências aí contidas), descrita como:
é o raio característico do disco.
Para a componente bojo, a função mais utilizada é aquela sugerida por de Vaucouleurs (ver Caon, Capaccioli &
D'Onofrio 1993 e referências aí contidas), descrita como:
![\begin{displaymath}
{\Sigma_{b}(r)} = {\Sigma_{e} 10^{-3.33[{(r/r_{e})}^{1/4}-1]}},
\end{displaymath}](img146.png) |
(29) |
em luminosidade, ou:
![\begin{displaymath}
{\mu_{b}(r)} = {\mu_{e} + 8.325 [{(r/r_{e})}^{1/4} - 1]},
\end{displaymath}](img147.png) |
(30) |
em magnitudes. Enquanto 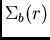 e
e 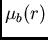 indicam o brilho superficial do bojo em função da
distância galactocêntrica
indicam o brilho superficial do bojo em função da
distância galactocêntrica 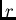 ,
, 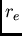 é o raio efetivo do bojo, i.e., aquele que contém metade da
luminosidade total da galáxia.
é o raio efetivo do bojo, i.e., aquele que contém metade da
luminosidade total da galáxia. 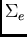 e
e 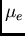 representam o brilho superficial efetivo, i.e., aquele
na distância galactocêntrica
representam o brilho superficial efetivo, i.e., aquele
na distância galactocêntrica 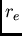 .
Embora a lei de de Vaucouleurs represente bem o perfil de brilho
para galáxias elípticas, e também para alguns bojos, vários trabalhos mostraram que alguns
bojos são melhor representados por um perfil
puramente exponencial (e.g., de Jong 1996a). Nesse caso, torna-se interessante utilizar o perfil generalizado
de de Vaucouleurs, proposto por Sérsic (Caon, Capaccioli & D'Onofrio 1993 e referências aí contidas).
O perfil de Sérsic é descrito como:
.
Embora a lei de de Vaucouleurs represente bem o perfil de brilho
para galáxias elípticas, e também para alguns bojos, vários trabalhos mostraram que alguns
bojos são melhor representados por um perfil
puramente exponencial (e.g., de Jong 1996a). Nesse caso, torna-se interessante utilizar o perfil generalizado
de de Vaucouleurs, proposto por Sérsic (Caon, Capaccioli & D'Onofrio 1993 e referências aí contidas).
O perfil de Sérsic é descrito como:
![\begin{displaymath}
{\Sigma_{b}(r)} = {\Sigma_{e} 10^{-b_{n}[{(r/r_{e})}^{1/n}-1]}},
\end{displaymath}](img153.png) |
(31) |
em luminosidade, ou:
![\begin{displaymath}
{\mu_{b}(r)} = {\mu_{e} + c_{n} [{(r/r_{e})}^{1/n} - 1]},
\end{displaymath}](img154.png) |
(32) |
em magnitudes, onde
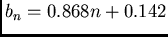 , e
, e
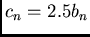 , com
, com 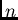 denominado por índice
de Sérsic. No caso em que
denominado por índice
de Sérsic. No caso em que 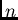 é igual a 4, temos a conhecida lei de de Vaucouleurs, enquanto que
é igual a 4, temos a conhecida lei de de Vaucouleurs, enquanto que  nos fornece uma lei exponencial semelhante àquela utilizada para descrever discos.
A inserção de mais um parâmetro livre para representar os perfis radiais de brilho superficial de galáxias
espirais certamente produz melhores ajustes. Porém, uma motivação maior para se utilizar o perfil de Sérsic
vem do fato de que o índice
nos fornece uma lei exponencial semelhante àquela utilizada para descrever discos.
A inserção de mais um parâmetro livre para representar os perfis radiais de brilho superficial de galáxias
espirais certamente produz melhores ajustes. Porém, uma motivação maior para se utilizar o perfil de Sérsic
vem do fato de que o índice 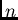 parece se correlacionar com alguns parâmetros fundamentais de galáxias, tais
como a razão bojo/disco (Andredakis, Peletier & Balcells 1995).
Como já foi mencionado, utilizamos um programa (de Souza 1997) para realizar a
decomposição bojo/disco bi-dimensional nas 39 galáxias de nossa sub-amostra, adotando a
equação 3.2 para a componente disco,
e a equação 3.6 para a componente bojo. As imagens utilizadas por este programa são as imagens linearizadas do
DSS, transformadas em uma matriz de dados, na qual cada posição (linha/coluna) representa um ``pixel'' da
imagem, com o valor da intensidade no ``pixel'' correspondente.
Entretanto, para que o programa possa executar corretamente a minimização dos erros durante a decomposição,
é necessário multiplicar a imagem do DSS em intensidade (linearizada e normalizada pelo fundo de céu local)
por uma constante, de modo a converter o ruído estatístico na imagem em um ruído de caráter Poissônico,
tal como em uma observação direta.
Assim, definindo
parece se correlacionar com alguns parâmetros fundamentais de galáxias, tais
como a razão bojo/disco (Andredakis, Peletier & Balcells 1995).
Como já foi mencionado, utilizamos um programa (de Souza 1997) para realizar a
decomposição bojo/disco bi-dimensional nas 39 galáxias de nossa sub-amostra, adotando a
equação 3.2 para a componente disco,
e a equação 3.6 para a componente bojo. As imagens utilizadas por este programa são as imagens linearizadas do
DSS, transformadas em uma matriz de dados, na qual cada posição (linha/coluna) representa um ``pixel'' da
imagem, com o valor da intensidade no ``pixel'' correspondente.
Entretanto, para que o programa possa executar corretamente a minimização dos erros durante a decomposição,
é necessário multiplicar a imagem do DSS em intensidade (linearizada e normalizada pelo fundo de céu local)
por uma constante, de modo a converter o ruído estatístico na imagem em um ruído de caráter Poissônico,
tal como em uma observação direta.
Assim, definindo 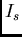 como a intensidade do céu (
como a intensidade do céu ( ), e
), e 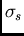 o seu desvio padrão absoluto,
precisamos multiplicar a imagem com valores em intensidade
o seu desvio padrão absoluto,
precisamos multiplicar a imagem com valores em intensidade 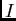 por uma constante
por uma constante 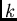 , obtendo então valores em
contagens:
, obtendo então valores em
contagens:  . As contagens do céu seguirão a mesma expressão:
. As contagens do céu seguirão a mesma expressão:
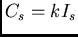 , e o seu desvio
padrão absoluto (i.e., o ruído na imagem), em contagens, é:
, e o seu desvio
padrão absoluto (i.e., o ruído na imagem), em contagens, é:
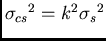 .
Para que
.
Para que 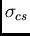 obedeça a estatística de Poisson, deve seguir a expressão:
obedeça a estatística de Poisson, deve seguir a expressão:
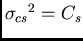 . Portanto, temos:
. Portanto, temos:
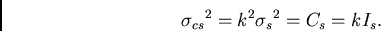 |
(33) |
Assim, podemos determinar 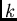 :
:
 |
(34) |
O valor da intensidade do céu, 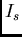 , o desvio padrão absoluto do céu, em intensidade,
, o desvio padrão absoluto do céu, em intensidade, 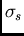 ,
bem como a constante
,
bem como a constante 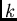 , são determinados separadamente para cada galáxia, através da tarefa
IMSTATISTICS do pacote IRAF (``Image Reduction & Analysis Facility''). Esta tarefa foi aplicada
em 5 regiões distintas de cada imagem, nas quais se observa, essencialmente, somente o fundo de céu.
Os valores medianos de cada parâmetro foram adotados. Antes de executar o programa,
ainda é necessário subtrair a contribuição do fundo de céu. Para tanto, simplesmente subtraímos da
imagem a constante
, são determinados separadamente para cada galáxia, através da tarefa
IMSTATISTICS do pacote IRAF (``Image Reduction & Analysis Facility''). Esta tarefa foi aplicada
em 5 regiões distintas de cada imagem, nas quais se observa, essencialmente, somente o fundo de céu.
Os valores medianos de cada parâmetro foram adotados. Antes de executar o programa,
ainda é necessário subtrair a contribuição do fundo de céu. Para tanto, simplesmente subtraímos da
imagem a constante
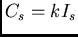 . Além disso, objetos que não fazem parte de nossa análise, tais como,
estrelas e galáxias de fundo (bem como defeitos na imagem), são retirados da imagem, através da tarefa
IMEDIT do IRAF.
O programa contém vários parâmetros de entrada a serem fornecidos pelo usuário, entre eles:
. Além disso, objetos que não fazem parte de nossa análise, tais como,
estrelas e galáxias de fundo (bem como defeitos na imagem), são retirados da imagem, através da tarefa
IMEDIT do IRAF.
O programa contém vários parâmetros de entrada a serem fornecidos pelo usuário, entre eles:
- o tamanho do ``pixel'' em segundos de arco (igual a 1.7 para as imagens do DSS);
- os valores iniciais das coordenadas do centro da galáxia;
- os valores iniciais do brilho superficial central do disco e do brilho superficial efetivo do bojo;
- os valores iniciais do raio característico do disco e do raio efetivo do bojo;
- os valores iniciais do ângulo de posição e da elipticidade de bojo e disco;
- o valor inicial do índice de Sérsic;
- e o valor do ``seeing'' (adotado como sendo igual a 1 ``pixel'').
Com estes valores e a matriz de dados correspondente à imagem da galáxia, o programa procura ajustar os
perfis de disco e bojo (i.e., as equações 3.2 e 3.6, respectivamente), variando não somente os parâmetros dos
perfis, mas também os parâmetros geométricos (elipticidade e ângulo de posição). A variação
destes parâmetros é controlada de modo a maximizar a qualidade do ajuste. No ajuste, considera-se que
as isofotas dos bojos e discos são elipses perfeitas, e que o disco se extende até o centro da galáxia. Assumimos
que não existem erros residuais relativos à subtração do céu, mas apenas um ruído
de caráter Poissônico na matriz de dados. Quando a variação na qualidade do ajuste cai abaixo de um certo
limite de convergência, o programa é interrompido, gerando os parâmetros a seguir:
- os valores finais do brilho superficial central do disco e do brilho superficial efetivo do bojo;
- os valores finais do raio característico do disco e do raio efetivo do bojo;
- o valor final do índice de Sérsic;
- e as razões entre as luminosidades e os diâmetros de bojo e disco.
Desta forma, o programa é aplicado para cada galáxia cerca de 3 a 5 vezes, tipicamente. Isso porque é
necessário variar os valores iniciais dos parâmetros de entrada, até encontrar o ajuste mais satisfatório.
Isto decorre do caráter altamente não linear dos perfis de brilho, que, em alguns casos, gera soluções espúrias.
Por exemplo, se existem barras ou braços espirais, a orientação do eixo maior da galáxia tende a sofrer
variações muito bruscas, particularmente se esta está sendo vista de face.
É comum encontrar na literatura decomposições bojo/disco que utilizam somente uma dimensão ao longo da
imagem da galáxia, em geral ao longo do seu eixo-maior. De toda a informação contida na imagem completa
da galáxia, extrai-se um valor característico para se construir um perfil que se ajuste em uma única
direção. Este método tem a vantagem de aumentar a razão sinal/ruído, mas perde toda a informação
presente na imagem da galáxia, relativa a componentes não-axissimétricas, como barras, por
e-xemplo. O ajuste bi-dimensional de modelos a imagens de galáxias tem poucos exemplos na literatura
(e.g., de Jong 1996a e referências aí contidas). Apesar de o modelo utilizado neste trabalho não incluir uma barra,
a técnica utilizando um ajuste bi-dimensional é certamente mais confiável do que um método uni-dimensional,
não somente para galáxias barradas, que correspondem a 85% das galáxias em nossa sub-amostra, mas
para galáxias em geral.
Com os parâmetros dos perfis ajustados, o programa constrói imagens artificiais da galáxia modelo,
bem como do bojo e do disco separadamente. Em seguida, utilizando a tarefa ELLIPSE do IRAF,
construímos os perfis de brilho da galáxia original, da galáxia modelo, do bojo e do disco, além
dos perfis de elipticidade, ângulo de posição e do coeficiente de Fourier b4, para a galáxia
original e para a galáxia modelo. O comportamento do coeficiente b4 indica o quanto as isofotas da
galáxia são distintas de uma elipse perfeita. Um valor positivo para b4 indica isofotas com uma
sub-componente ``disky'', enquanto que um valor negativo indica isofotas ``boxy''. Se b4 é igual a 0,
então a isofota é uma elipse perfeita. Todo esse procedimento nos permite avaliar a qualidade do
ajuste determinado pelo programa e ainda outros parâmetros estruturais da galáxia. Além disso,
subtraímos da imagem original as imagens sintéticas, obtendo imagens residuais, com o objetivo de
avaliar eventuais sub-estruturas.
A Figura 3.1 exibe os resultados da decomposição bojo/disco para a galáxia NGC 488, como um exemplo.
Nesta figura, temos, da esquerda para a direita e de cima para baixo:
- imagem original (passada por um filtro mediano e transformada para brilho superficial) com o mapa
isofotal sobreposto;
- imagem residual total (imagem original
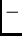 modelo completo);
modelo completo);
- imagem residual do disco (imagem original
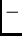 modelo do bojo);
modelo do bojo);
- imagem residual do bojo (imagem original
 modelo do disco);
modelo do disco);
- perfis de brilho na banda V (em magnitudes por segundo de arco ao quadrado em função do raio em
``pixels''):
- pontos com barras de erro: imagem original;
- linha com traços curtos: modelo do disco;
- linha com traços longos: modelo do bojo;
- linha cheia: modelo completo;
- pontos com linha cheia: resíduo total em magnitudes por segundo de arco ao quadrado
(imagem original - modelo + 28);
- perfis de elipticidade:
- pontos com barras de erro: imagem original;
- linha cheia: modelo completo;
- perfis do ângulo de posição:
- pontos com barras de erro: imagem original;
- linha cheia: modelo completo;
- perfis do coeficiente de Fourier b4:
- pontos com barras de erro: imagem original;
- linha cheia: modelo completo;
Para calibrar nossos dados, de modo a deixar nossos perfis compatíveis com as magnitudes observadas
na literatura para as galáxias em nossa sub-amostra, utilizamos a tarefa IMEXAMINE do IRAF.
Com a tarefa IMEXAMINE, calculamos a magnitude da galáxia, na imagem em contagens, em sete valores
distintos de abertura, comparando os resultados com a magnitude V aparente publicada em LdV83,85 para as
mesmas aberturas. A constante de calibração 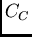 para cada galáxia é tomada como sendo a mediana
das diferenças entre essas magnitudes, somada à constante de transformação para brilho superficial
e subtraindo o termo de correção para a extinção Galáctica (ver seção 2.3.1), utilizando os mapas
de Schlegel, Finkbeiner & Davis (1998). Assim,
para cada galáxia é tomada como sendo a mediana
das diferenças entre essas magnitudes, somada à constante de transformação para brilho superficial
e subtraindo o termo de correção para a extinção Galáctica (ver seção 2.3.1), utilizando os mapas
de Schlegel, Finkbeiner & Davis (1998). Assim,
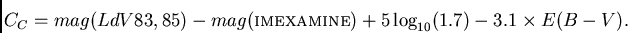 |
(35) |
Figure:
Resultados da decomposição bojo/disco para a galáxia Sb(r) NGC 488. No alto está especificada a
dimensão das imagens em segundos de arco. Para legendas, ver texto.
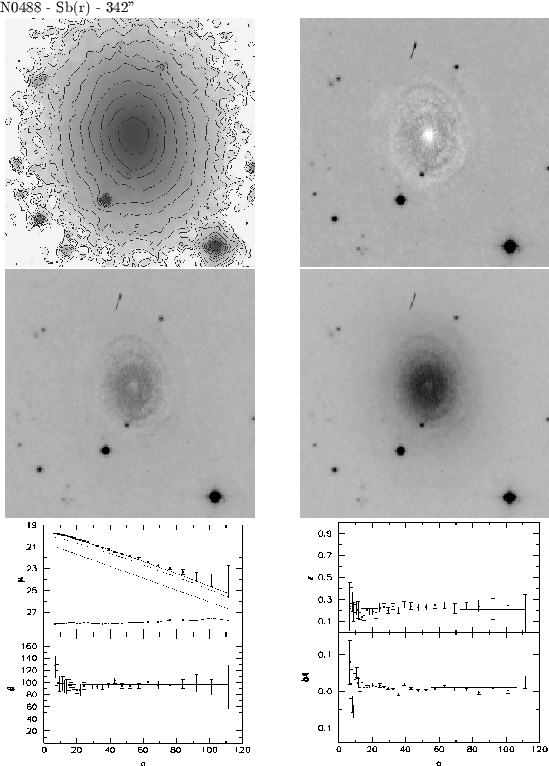 |
Muita informação pode ser extraída da Fig. 3.1. Em relação às imagens, vê-se prontamente que o bojo é
dominante nessa galáxia. De fato, NGC 488 apresenta a maior razão entre as luminosidades de bojo e disco
(igual a 3.1) entre as galáxias de nossa sub-amostra. Também se verifica que os braços espirais
são mais aparentes nas imagens residuais, o que
é esperado, já que os braços não são ajustados no modelo. Os perfis mostram que o ajuste
alcançado é muito bom, e que o bojo segue um perfil puramente exponencial, semelhante ao disco.




Next: 4 Resultados
Up: 3 Fotometria Superficial
Previous: 2 As imagens do
Contents
Dimitri Gadotti
2003-10-06
