Descrever o movimento de um número ![]() de corpos sob a influência única da lei da
gravitação de Newton é o que se chama de problema gravitacional de
de corpos sob a influência única da lei da
gravitação de Newton é o que se chama de problema gravitacional de ![]() -corpos.
Matematicamente, isso equivale a determinar a posição
-corpos.
Matematicamente, isso equivale a determinar a posição ![]() e a velocidade
e a velocidade ![]() de
cada um dos corpos em função do tempo
de
cada um dos corpos em função do tempo ![]() e das condições iniciais do problema, quais sejam,
e das condições iniciais do problema, quais sejam,
![]() ,
, ![]() e
e
![]() , considerando que a única força atuante no sistema é a
força gravitacional entre os corpos, dada por:
, considerando que a única força atuante no sistema é a
força gravitacional entre os corpos, dada por:
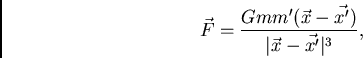 |
(29) |
onde ![]() é a constante da gravitação de Newton e
é a constante da gravitação de Newton e ![]() se refere à massa de cada
corpo. Note ainda que as variáveis com e sem linha se referem a corpos distintos e o ponto
denota a derivada temporal.
se refere à massa de cada
corpo. Note ainda que as variáveis com e sem linha se referem a corpos distintos e o ponto
denota a derivada temporal.
As regras básicas no jogo do problema gravitacional de ![]() -corpos foram estabelecidas por Newton
(1687) com a definição rigorosa de conceitos como posição, tempo, distância, velocidade,
aceleração, força, momento e energia. Com a contribuição de Newton podemos resolver o
problema quando
-corpos foram estabelecidas por Newton
(1687) com a definição rigorosa de conceitos como posição, tempo, distância, velocidade,
aceleração, força, momento e energia. Com a contribuição de Newton podemos resolver o
problema quando ![]() , i.e., o movimento de um corpo sob a ação de uma força externa qualquer.
Também podemos obter vários parâmetros físicos relevantes, obtendo informações
importantes, para qualquer que seja
, i.e., o movimento de um corpo sob a ação de uma força externa qualquer.
Também podemos obter vários parâmetros físicos relevantes, obtendo informações
importantes, para qualquer que seja ![]() . Passando para
. Passando para ![]() , a complexidade do problema já
aumenta muito, e só existe uma solução geral para corpos pontuais (partículas) ou esféricos
(ver, e.g., Bhatnagar & Saha 1993). O problema de 2 corpos foi particularmente importante para
o desenvolvimento inicial da Mecânica Celeste. Logo após Newton, o problema foi atacado para
resolver o movimento do sistema Terra-Lua. No entanto, esse desenvolvimento inicial encontrou
sérios problemas ao desconsiderar a perturbação do Sol.
, a complexidade do problema já
aumenta muito, e só existe uma solução geral para corpos pontuais (partículas) ou esféricos
(ver, e.g., Bhatnagar & Saha 1993). O problema de 2 corpos foi particularmente importante para
o desenvolvimento inicial da Mecânica Celeste. Logo após Newton, o problema foi atacado para
resolver o movimento do sistema Terra-Lua. No entanto, esse desenvolvimento inicial encontrou
sérios problemas ao desconsiderar a perturbação do Sol.
Galgando somente mais um degrau já chegamos ao limiar do nosso conhecimento. O problema de
3 corpos não possui solução geral analítica exata, embora esteja demonstrada a
existência desta solução (ver Hagihara 1970). Solução há (doravante considerando apenas
partículas) para o chamado problema de 3 corpos restrito. O que se faz é considerar que o
terceiro corpo possui massa infinitesimal, de forma a não afetar o movimento dos outros dois
corpos. Outras aproximações incluem assumir que o movimento do terceiro corpo está restrito ao
plano de movimento dos outros dois corpos. Para ![]() os formalismos introduzidos por Euler,
Lagrange e Hamilton nos fornecem as únicas soluções analíticas, que, entretanto, são
extremamente particulares.
os formalismos introduzidos por Euler,
Lagrange e Hamilton nos fornecem as únicas soluções analíticas, que, entretanto, são
extremamente particulares.
O desenvolvimento da Mecânica Celeste continuou através do desenvolvimento matemático da chamada Teoria das Perturbações. Imaginemos o problema de 3 corpos representado pelo sistema Sol-Terra-Lua. Enquanto a influência do Sol é tratada como uma perturbação, Terra e Lua são consideradas partículas cujo centro de massa tem uma órbita Kepleriana em torno do Sol. Tudo o que entra nos termos perturbativos são (além da massa do corpo perturbador) as distâncias entre os três corpos, mas estas são complicadas funções dos ângulos entre os corpos, especialmente se o movimento não for confinado a um plano (ver Goldstein 1950). Usualmente, os termos são expressos em séries de Fourier dos ângulos, mas, por sua vez, estes são séries complicadas expressas em termos dos elementos orbitais de Kepler e do tempo. Como resultado, temos uma intrincada série trigonométrica. Os métodos na Teoria das Perturbações tornam-se cada vez mais refinados, mas jamais deixaram de resultar em séries trigonométricas e, infelizmente, como foi provado por Poincaré, essas séries não são convergentes. Assim, embora estas séries representem uma solução ainda que aproximada, certamente não são a solução real do problema.
Muito do formalismo matemático da Mecânica Celeste, entretanto, é de pouca utilidade para a
Dinâmica Estelar, que trata de sistemas com um número espetacularmente excessivo de corpos.
Por outro lado, a Dinâmica Estelar tem uma conexão fundamental com a Mecânica Estatística
Clássica, já que o número de estrelas em um sistema estelar típico é grande o suficiente para
que seja necessário um tratamento estatístico da dinâmica do sistema. Além disso, uma grande
parte das ferramentas matemáticas utilizadas no desenvolvimento inicial da Dinâmica Estelar tem
origem na Física de Plasmas, que também envolve o estudo de um número muito grande de
partículas interagindo via forças de longo alcance (com relação ao tamanho do sistema).
Na próxima seção, veremos brevemente
o tratamento matemático do problema de ![]() -corpos em sistemas estelares, passo fundamental antes
de atacarmos as simulações numéricas.
-corpos em sistemas estelares, passo fundamental antes
de atacarmos as simulações numéricas.