Consideremos um sistema constituído por ![]() partículas.
A técnica mais simples possível na análise da evolução de um tal sistema é
realizar o cálculo das forças envolvidas (ou acelerações) diretamente. Tal método é
por vezes chamado de integração direta ou método PP (``particle-particle'' - partícula-partícula). Consiste
em resolver numericamente a seguinte equação de movimento para cada partícula
partículas.
A técnica mais simples possível na análise da evolução de um tal sistema é
realizar o cálculo das forças envolvidas (ou acelerações) diretamente. Tal método é
por vezes chamado de integração direta ou método PP (``particle-particle'' - partícula-partícula). Consiste
em resolver numericamente a seguinte equação de movimento para cada partícula ![]() :
:
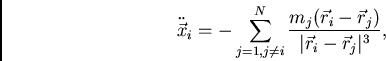 |
(76) |
onde ![]() e
e ![]() se referem a partículas distintas.17
se referem a partículas distintas.17
É evidente que o tempo dispendido no cálculo cresce muito com ![]() ; de fato, o tempo é
; de fato, o tempo é
![]() . Assim, é necessário que os métodos numéricos de
integração sejam eficientes. Em geral, as
. Assim, é necessário que os métodos numéricos de
integração sejam eficientes. Em geral, as ![]() equações diferenciais de segunda ordem são
re-escritas como
equações diferenciais de segunda ordem são
re-escritas como ![]() equações diferenciais de primeira ordem equivalentes. Depois, estas
são resolvidas numericamente através de um esquema do tipo Runge-Kutta (ou Euler,
ver, e.g., Humes et al. 1984), fornecendo
as equações para as novas posições e velocidades para cada partícula, calculadas a cada passo
de tempo definido. Preferencialmente, o passo de tempo não deve
ser constante, evidentemente. Na medida em que
as partículas se aproximam, as acelerações tornam-se muito grandes e, se computadas por um
tempo demasiado longo, as partículas percorrerão um espaço muito maior do que aquele
em um sistema real (já que as forças neste caso também variam muito rapidamente). Portanto,
se o passo de tempo for mantido constante os erros poderão ser
muito grandes quando as partículas
se aproximam. Assim, um esquema com passos de tempo variáveis deve ser utilizado, o qual
deve diminuir o passo na medida em que as partículas se aproximam.
equações diferenciais de primeira ordem equivalentes. Depois, estas
são resolvidas numericamente através de um esquema do tipo Runge-Kutta (ou Euler,
ver, e.g., Humes et al. 1984), fornecendo
as equações para as novas posições e velocidades para cada partícula, calculadas a cada passo
de tempo definido. Preferencialmente, o passo de tempo não deve
ser constante, evidentemente. Na medida em que
as partículas se aproximam, as acelerações tornam-se muito grandes e, se computadas por um
tempo demasiado longo, as partículas percorrerão um espaço muito maior do que aquele
em um sistema real (já que as forças neste caso também variam muito rapidamente). Portanto,
se o passo de tempo for mantido constante os erros poderão ser
muito grandes quando as partículas
se aproximam. Assim, um esquema com passos de tempo variáveis deve ser utilizado, o qual
deve diminuir o passo na medida em que as partículas se aproximam.
O código de árvore (``tree code'')
ou código hierárquico se baseia no fato de que as contribuições
para a força, em uma dada partícula, vindas de um conjunto de partículas distantes, podem ser
calculadas agrupadamente. Isto porque as tais contribuições são bastante similares se o grupo
de partículas estiver suficientemente distante. Inicialmente, cria-se uma estrutura hierárquica
de subdivisões em células cúbicas. A primeira célula contém todo o sistema,
e é recursivamente subdividida em oito novas células (duas para cada dimensão),
cada vez que é encontrada mais de uma partícula em uma célula (ver Barnes & Hut 1986).
Depois, para cada célula, é calculado o centro de massa e a massa total. Em seguida,
a aceleração em cada partícula é calculada segundo o seguinte critério. Definimos o ângulo
de tolerância (ou ângulo de abertura)
![]() , onde
, onde ![]() é a dimensão da célula que contém as partículas
atuantes, e
é a dimensão da célula que contém as partículas
atuantes, e ![]() é a distância entre o centro de massa da célula e a partícula sobre a qual
as forças estão sendo calculadas. Então, se
é a distância entre o centro de massa da célula e a partícula sobre a qual
as forças estão sendo calculadas. Então, se ![]() é maior do que um determinado
valor a ser escolhido (usualmente da ordem da unidade), as acelerações são calculadas
diretamente. Mas, caso contrário, as forças são calculadas assumindo que há apenas uma
partícula atuante na célula, com a respectiva massa total e na posição do centro de massa
previamente calculados.
é maior do que um determinado
valor a ser escolhido (usualmente da ordem da unidade), as acelerações são calculadas
diretamente. Mas, caso contrário, as forças são calculadas assumindo que há apenas uma
partícula atuante na célula, com a respectiva massa total e na posição do centro de massa
previamente calculados.
A estrutura da árvore precisa ser refeita a cada passo de tempo, mas, mesmo assim,
o tempo de cálculo cresce com ![]() , i.e., sensivelmente mais rápido que a integração
direta. Note que quanto menor o valor fixo escolhido para o ângulo de tolerância, maior será a
quantidade de forças calculadas pela integração direta. Isso aumenta o tempo de cálculo, mas,
por outro lado, produz melhores resultados, de forma que é preciso buscar um compromisso.
, i.e., sensivelmente mais rápido que a integração
direta. Note que quanto menor o valor fixo escolhido para o ângulo de tolerância, maior será a
quantidade de forças calculadas pela integração direta. Isso aumenta o tempo de cálculo, mas,
por outro lado, produz melhores resultados, de forma que é preciso buscar um compromisso.
Considerar que o potencial devido às partículas numa determinada célula possa ser representado pelo potencial provocado por uma pseudo-partícula com a massa total no interior da célula, e no centro de massa da mesma, é o mesmo que se faz em Eletromagnetismo ao se expandir o potencial elétrico em multipolos (ver, e.g., Reitz, Milford & Christy 1980). Porém, neste caso, inclui-se apenas o primeiro termo da expansão (monopolo). Assim, se considerarmos momentos de quadrupolo, por exemplo, na construção das pseudo-partículas, o cálculo de forças será mais exato. Tal implementação já existe em alguns códigos hierárquicos.
Considerar passos de tempo não constantes não é tão trivial. Uma forma de se fazer isso é dividir pela metade o passo de tempo sempre que necessário, i.e., sempre que as forças ultrapassem determinado limite. Entretanto, a definição deste limite é difícil na medida em que pode aumentar muito o tempo de cálculo. E implica, também, em estender a hierarquia da árvore de três dimensões espaciais para a dimensão temporal.
Outro esquema comumente utilizado para a resolução numérica da Eq. (3.48) é o
``leapfrog''.18Este esquema é particularmente utilizado em simulações cosmológicas de formação de estruturas
em larga escala. Este esquema é menos preciso do que os esquemas de ordem superior de
Runge-Kutta. Sua vantagem, no entanto, está no fato de que necessita o armazenamento de
um número menor de variáveis e, portanto, é mais rápido. Neste esquema, posições
e velocidades são calculadas fora de fase por meio passo de tempo. Definindo o ![]() -ésimo
passo de tempo como
-ésimo
passo de tempo como
![]() , onde
, onde ![]() é o passo de tempo e
é o passo de tempo e ![]() é o tempo inicial,
então o esquema procede da seguinte forma. As posições das partículas em
é o tempo inicial,
então o esquema procede da seguinte forma. As posições das partículas em ![]() são
utilizadas para calcular as forças
são
utilizadas para calcular as forças ![]() . Estas forças são então utilizadas para
avançar as velocidades das partículas em
. Estas forças são então utilizadas para
avançar as velocidades das partículas em ![]() para novos valores em
para novos valores em ![]() . Assim,
temos:
. Assim,
temos:
| (77) |
Então, as novas velocidades são utilizadas para atualizar as posições das partículas
no passo de tempo ![]() :
:
| (78) |
Assim, as posições e velocidades das partículas nunca são conhecidas no mesmo instante de tempo.
Aarseth (1972, 1985) elaborou um esquema para o cálculo numérico da Eq. (3.48) que permite
o uso de passos de tempo individuais. Trata-se de expandir a força em um polinômio de
quarta ordem em termos de um intervalo de tempo ![]() , que é re-escrito como uma função
explícita do passo de tempo. Colocando a restrição de que as forças calculadas só são
válidas quando o polinômio convirja bem, então as posições e velocidades de cada partícula
são calculadas com passos de tempo individuais. Além disso, somente quando o passo de tempo
é pequeno o suficiente, para que o tratamento do problema seja adequado a curtas distâncias,
as forças serão computadas.
, que é re-escrito como uma função
explícita do passo de tempo. Colocando a restrição de que as forças calculadas só são
válidas quando o polinômio convirja bem, então as posições e velocidades de cada partícula
são calculadas com passos de tempo individuais. Além disso, somente quando o passo de tempo
é pequeno o suficiente, para que o tratamento do problema seja adequado a curtas distâncias,
as forças serão computadas.
Na maioria dos casos, quando não se quer fazer avaliações sobre sistemas colisionais, é
utilizado um parâmetro de suavização (``softening''), ![]() , para evitar forças
infinitas a curtíssimas distâncias. Assim, a equação de força fica como:
, para evitar forças
infinitas a curtíssimas distâncias. Assim, a equação de força fica como:
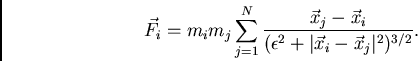 |
(79) |
As forças portanto têm um limite superior, e essa é uma das maiores fraquezas das
simulações ![]() -corpos, já que a força deixa de ser exatamente Newtoniana. Esta
discrepância, entretanto, deixa de ser significativa se
-corpos, já que a força deixa de ser exatamente Newtoniana. Esta
discrepância, entretanto, deixa de ser significativa se ![]() for escolhido
adequadamente. A importância de
for escolhido
adequadamente. A importância de ![]() vem do seguinte.
Sabemos que galáxias, por exemplo, são sistemas estelares nos quais a relaxação a
dois corpos não tem um papel relevante (ver seção anterior). Isto por causa do grande número de estrelas.
Como não nos é possível realizar simulações com
vem do seguinte.
Sabemos que galáxias, por exemplo, são sistemas estelares nos quais a relaxação a
dois corpos não tem um papel relevante (ver seção anterior). Isto por causa do grande número de estrelas.
Como não nos é possível realizar simulações com ![]() partículas, as galáxias
simuladas têm da ordem de
partículas, as galáxias
simuladas têm da ordem de ![]() a
a ![]() partículas.19 Assim, nas galáxias simuladas
o tempo de relaxação seria muito menor do que em galáxias reais se não usássemos
o parâmetro de suavização. O parâmetro
partículas.19 Assim, nas galáxias simuladas
o tempo de relaxação seria muito menor do que em galáxias reais se não usássemos
o parâmetro de suavização. O parâmetro ![]() funciona diminuindo a granulosidade do sistema,
tornando-o mais contínuo. Assim, um sistema granuloso como um disco de
funciona diminuindo a granulosidade do sistema,
tornando-o mais contínuo. Assim, um sistema granuloso como um disco de ![]() partículas
pode representar bem um disco estelar real, muito menos granuloso, com
partículas
pode representar bem um disco estelar real, muito menos granuloso, com ![]() estrelas. O parâmetro de suavização, colocado desta forma, faz com que cada
partícula seja tratada de fato como uma esfera de Plummer (1911), cuja distribuição
de massa é finita, e para a qual 85% da massa está contida dentro de um raio igual a
estrelas. O parâmetro de suavização, colocado desta forma, faz com que cada
partícula seja tratada de fato como uma esfera de Plummer (1911), cuja distribuição
de massa é finita, e para a qual 85% da massa está contida dentro de um raio igual a
![]() . Note que o parâmetro de suavização coloca um limite máximo para a
resolução espacial durante o experimento numérico.
. Note que o parâmetro de suavização coloca um limite máximo para a
resolução espacial durante o experimento numérico.
Na verdade, em sistemas colisionais também deve ser introduzido um parâmetro de
suavização. Seria ideal não utilizar ![]() neste casos, já que estes sistemas são, em
geral, granulosos, mesmo na natureza. No entanto, o problema das forças infinitas nos força
a impôr a suavização.
neste casos, já que estes sistemas são, em
geral, granulosos, mesmo na natureza. No entanto, o problema das forças infinitas nos força
a impôr a suavização.
Outra técnica assaz eficiente e utilizada é o método PM (``particle-mesh''
- partícula-reticulado). Como o nome indica, este
método aproxima as forças utilizando uma rede fina. O que se faz, essencialmente,
é atribuir aos pontos do reticulado mais próximos de uma dada partícula um valor proporcional
à massa da partícula. Existem vários esquemas distintos para realizar esta atribuição.
Com essa aproximação, resolve-se a equação de Poisson [Eq. (3.42)] no reticulado, em geral,
utilizando a técnica de transformada rápida de Fourier (ver, e.g., Boas 1966, Press et al. 1992).
E, a partir deste potencial no reticulado,
é calculado o campo de forças no reticulado, e as forças em cada partícula são calculadas
por interpolação. Em seguida, o procedimento é o padrão: calcula-se as novas velocidades
e posições para cada partícula e reinicia-se o processo. Uma diferença importante a se notar
com relação aos códigos de árvore é a de que o reticulado é fixo, o que, dependendo da
geometria do sistema, pode representar uma desvantagem. A principal vantagem do método PM
é a de ser muito mais rápido, e daí um número bem maior de partículas pode ser
utilizado. Entretanto, a resolução espacial (e, neste caso, também ![]() )
fica definida pela dimensão das células do reticulado.
)
fica definida pela dimensão das células do reticulado.
Vejamos agora alguns métodos híbridos, i.e., que se usam tanto de um reticulado quanto da
integração direta (ver Hockney & Eastwood 1988).
O primeiro deles é o método P![]() M (``particle-particle/particle-mesh'').
Este método soluciona um dos problemas do método PM, que é a imprecisão no cálculo
de forças de partículas próximas. Se um determinado par de partículas tiver uma separação
menor do que cerca de 3 vezes a dimensão de uma célula, então as forças envolvidas
são calculadas via integração direta. Em geral, usa o esquema ``leapfrog'' para atualizar
posições e velocidades. Uma desvantagem deste método é que muitas vezes os cálculos
por integração direta passam a dominar a evolução de um dado sistema. Para contornar este
problema, um algoritmo distinto foi desenvolvido: o método AP
M (``particle-particle/particle-mesh'').
Este método soluciona um dos problemas do método PM, que é a imprecisão no cálculo
de forças de partículas próximas. Se um determinado par de partículas tiver uma separação
menor do que cerca de 3 vezes a dimensão de uma célula, então as forças envolvidas
são calculadas via integração direta. Em geral, usa o esquema ``leapfrog'' para atualizar
posições e velocidades. Uma desvantagem deste método é que muitas vezes os cálculos
por integração direta passam a dominar a evolução de um dado sistema. Para contornar este
problema, um algoritmo distinto foi desenvolvido: o método AP![]() M (``adaptive P
M (``adaptive P![]() M'', ou
P
M'', ou
P![]() M adaptativo).
Neste último, um algoritmo hierárquico aumenta a densidade de células quando necessário
(baseando-se na densidade em número de partículas),
diminuindo assim a quantidade de forças calculadas pela integração direta. O método
AMR (``adaptive mesh refinement'', ou refinamento do reticulado adaptativo)
se utiliza do mesmo algoritmo, excluindo, porém, a parte
PP. O método TPM (``tree code particle-mesh''),
como o nome indica, é um híbrido, que usa um esquema de
árvore quando a densidade de partículas é alta, e um esquema PM quando a densidade
é baixa.
M adaptativo).
Neste último, um algoritmo hierárquico aumenta a densidade de células quando necessário
(baseando-se na densidade em número de partículas),
diminuindo assim a quantidade de forças calculadas pela integração direta. O método
AMR (``adaptive mesh refinement'', ou refinamento do reticulado adaptativo)
se utiliza do mesmo algoritmo, excluindo, porém, a parte
PP. O método TPM (``tree code particle-mesh''),
como o nome indica, é um híbrido, que usa um esquema de
árvore quando a densidade de partículas é alta, e um esquema PM quando a densidade
é baixa.
Outros métodos incluem o método PM![]() (``particle-multiple mesh'', ou
partícula-reticulado múltiplo) e o
método NGPM (``nested grid particle-mesh'', ou partícula-reticula-do em rede aninhada),
que não são híbridos, i.e., não
têm a parte PP, mas se utilizam de redes dentro de redes.
(``particle-multiple mesh'', ou
partícula-reticulado múltiplo) e o
método NGPM (``nested grid particle-mesh'', ou partícula-reticula-do em rede aninhada),
que não são híbridos, i.e., não
têm a parte PP, mas se utilizam de redes dentro de redes.
Um método que foge um pouco dos acima descritos, mas sobre o qual vale a pena tecer
alguns comentários, é o método de Monte Carlo, particularmente utilizado
na simulação de aglomerados estelares, pois tem um tratamento bastante eficaz das
colisões. Neste método (ver, e.g., Hénon 1972, 1975; Spitzer 1975), a órbita de cada
partícula é seguida numericamente, e perturbações pequenas e aleatórias são
aplicadas à velocidade da partícula ao longo de sua órbita. Essas perturbações
têm o intuito de mimetizar o efeito das colisões. Portanto, são escolhidas com
técnicas de Monte Carlo, de forma que sejam consistentes com os coeficientes de
difusão [ver Eq. (3.40)]. O número de partículas deve ser suficientemente grande para
que o erro estatístico seja pequeno. Usualmente ![]() . O método de Monte Carlo
é mais rápido que os códigos de
. O método de Monte Carlo
é mais rápido que os códigos de ![]() -corpos propriamente ditos, primeiro porque o
número de partículas é bem menor, e segundo, porque o número de operações
é proporcional a
-corpos propriamente ditos, primeiro porque o
número de partículas é bem menor, e segundo, porque o número de operações
é proporcional a ![]() . Apesar de hoje já podermos contar com simulações com
. Apesar de hoje já podermos contar com simulações com
![]() partículas, que é a ordem do número de estrelas em um aglomerado globular,
este método ainda permance promissor, já que não têm a necessidade de suavização
e pode ser utilizado para outros sistemas colisionais que possuem um número de
estrelas muito grande, como é o caso de núcleos de galáxias.
partículas, que é a ordem do número de estrelas em um aglomerado globular,
este método ainda permance promissor, já que não têm a necessidade de suavização
e pode ser utilizado para outros sistemas colisionais que possuem um número de
estrelas muito grande, como é o caso de núcleos de galáxias.
Em particular, os métodos que utilizam reticulados são utilizados para fazer simulações nas quais é mais importante ter um grande número de partículas do que uma boa resolução espacial. Este é o caso de simulações de formação de estruturas em larga escala no universo, ou formação de galáxias via o cenário hierárquico. Já para simulações de galáxias, que têm o objetivo de traçar a formação e evolução de estruturas galácticas, os códigos hierárquicos são os mais utilizados, pois permitem realizar simulações com alta resolução espacial.
Evidentemente, os métodos aqui descritos são apenas os mais utilizados, ou os mais importantes.
Em particular, métodos híbridos vêm sendo confeccionados para serem utilizados
especificamente em supercomputadores (com multiprocessadores paralelizados)
construídos com a especial finalidade de realizar simulações ![]() -corpos.
Embora haja outros métodos sendo utilizados e desenvolvidos, a essência da maior parte deles
não foge das técnicas aqui apresentadas.
-corpos.
Embora haja outros métodos sendo utilizados e desenvolvidos, a essência da maior parte deles
não foge das técnicas aqui apresentadas.