3 Cálculo dos gradientes de cor

Os gradientes de cor (U-B) e (B-V) das galáxias da amostra foram determinados através dos índices de cor (U-B) e (B-V) apresentados no LdV83,85 para várias aberturas distintas ao longo de cada galáxia.

Como o LdV83,85 é uma compilação de dados adquiridos por vários observadores, utilizando diferentes instrumentos e telescópios, e em diferentes condições atmosféricas, é natural que algumas medidas pareçam inconsistentes entre si, já que alguns dados podem estar mais perturbados por erros internos. Por exemplo, autores diferentes podem fornecer valores bastante distintos do índice (U-B) para a mesma galáxia e no diafragma de mesma abertura. De fato, este é o caso de NGC 2377 no diafragma de abertura de 2.6 minutos de arco, em que 3 fontes distintas atribuem ao índice (U-B) os valores 0.11, 0.20 e 0.38! Tentar ajustar uma reta ao gradiente de cor em magnitudes, assumindo que os índices de cor variam linearmente com o logaritmo da abertura, usando estes valores, através da mais comumente utilizada e clássica regressão linear pelo método dos Mínimos Quadrados (MQ), resultará em valores bastante incertos.

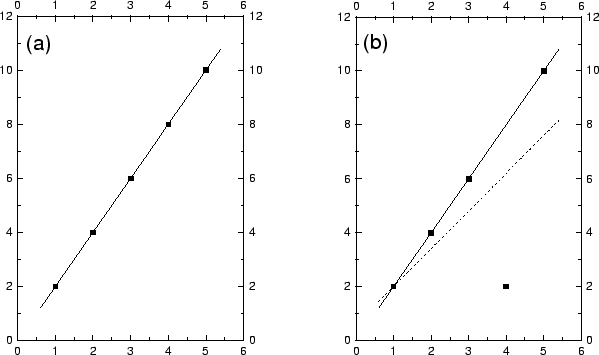
Assim sendo, torna-se muito importante o uso de técnicas estatísticas robustas para minimizar estas incertezas. Escolhemos aplicar o método da Mínima Mediana dos Quadrados (MMQ), que foi apresentado pela primeira vez por Rousseeuw (1984). Este método minimiza a mediana dos quadrados dos resíduos, no lugar da soma dos quadrados dos resíduos, como faz a clássica regressão linear pelo método dos mínimos quadrados. Os resultados obtidos podem resistir a até quase 50% de contaminação nos dados. A Figura 2.3 ilustra a robustez do método da mínima mediana (MMQ).

Figure: Um exemplo da robustez do método de regressão linear pela mínima mediana. Em (a), o resultado do ajuste ao conjunto de pontos é indiferente do método. Em (b), o método clássico (linha tracejada) é gravemente perturbado pela contaminação de um único ponto, enquanto que o método da mínima mediana (linha cheia) permanece atribuindo aos pontos o mesmo ajuste.

Para calcular os gradientes de cor das galáxias em nossa amostra, aplicamos o programa PROGRESS, desenvolvido por Rousseeuw & Leroy (1987). Este programa exe-cuta uma análise robusta da regressão linear, e além de usar o método MMQ, fornece parâmetros de regressão confiáveis, e permite identificar pontos que pareçam inconsistentes com o restante dos dados (``outliers''). PROGRESS primeiro determina os parâmetros da regressão através do método dos mínimos quadrados, e depois através do método da mínima mediana dos quadrados. Com esses resultados, o algoritmo é capaz de separar pontos que estejam contaminando os dados e, atribuindo-lhes peso zero, recalcula o gradiente através do método dos mínimos quadrados. Com este algoritmo, os gradientes obtidos têm, na maioria das vezes, os mesmos valores que aqueles obtidos quando se aplica somente o método da mínima mediana dos quadrados. No entanto, o método MQ trabalha melhor que o método MMQ nos casos em que o número de pontos não é grande, característica importante no caso de nossa amostra. Assim, o algoritmo adotado em PROGRESS fornece resultados mais confiáveis.

O cálculo de cada gradiente foi acompanhado cuidadosamente, pois, em alguns casos, o resultado da regressão pelo método clássico é mais representativo do gradiente da galáxia do que aquele obtido através do algoritmo de PROGRESS. Isto pode acontecer porque, ao tentar minimizar as incertezas, o método da mínima mediana pode caracterizar o gradiente global da galáxia utilizando somente alguns poucos pontos que se ajustam muito bem a uma linha reta. Nos casos em que este ajuste é muito bom, o algoritmo de PROGRESS não é capaz de recuperar o gradiente global da galáxia e descartar somente aqueles pontos que realmente são ``outliers''. Ao contrário, descarta todos os pontos que não satisfazem aquele excelente ajuste caracterizado por somente alguns poucos pontos. Portanto, em alguns casos, definimos o gradiente da galáxia como sendo aquele obtido pelo método clássico.

Das 257 galáxias de nossa amostra, obtivemos 239 gradientes de cor (B-V) e 202 (U-B). O restante dos gradientes foi desconsiderado, já que: (1) o número de medidas disponíveis é insuficiente para uma boa determinação do gradiente, e/ou (2) as medidas são demasiadamente inconsistentes, resultando em valores muito incertos para os gradientes. Os gradientes que determinamos para as galáxias de nossa amostra, bem como os respectivos erros, encontram-se na tabela A.1.

Figure: Exemplos de gradientes de cor para quatro galáxias em nossa amostra. O típico gradiente negativo de NGC 1425 e NGC 2613, o gradiente nulo de NGC 1672, e o raro gradiente positivo de UGC 3973 (confira os valores na Tabela A.1). Os índices de cor em magnitudes estão expressos em função do logaritmo da abertura do diafragma em unidades de 0.1 minutos de arco. Os quadrados indicam o índice (B-V), enquanto que os círculos indicam o (U-B). As linhas tracejadas correspondem ao ajuste através do método dos mínimos quadrados; linhas pontilhadas representam o ajuste pelo método da mínima mediana e a linha cheia corresponde ao ajuste determinado pelo algoritmo de PROGRESS.

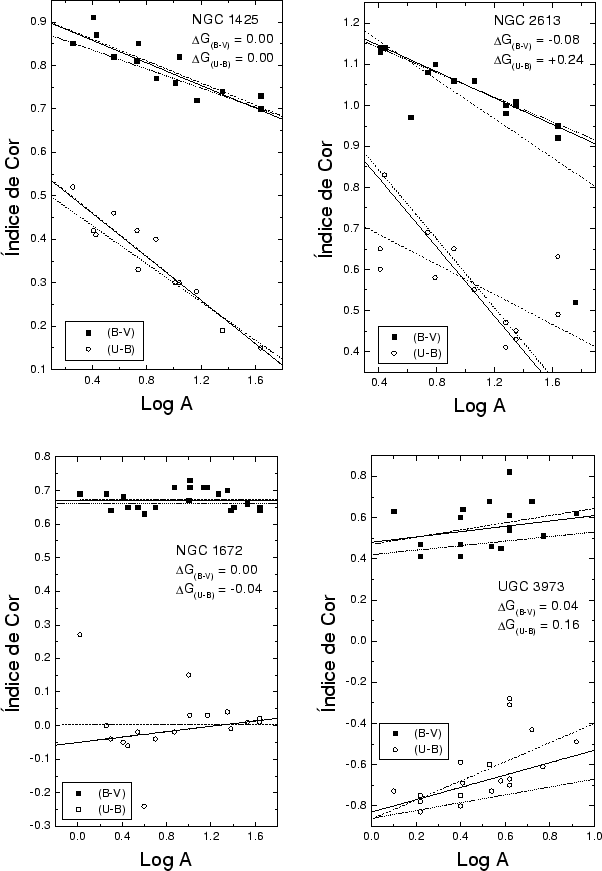A Figura 2.4 exibe quatro exemplos do comportamento dos gradientes de cor para galáxias da presente amostra. Nesta figura pode-se avaliar os ajustes dos gradientes através dos diferentes métodos. As linhas tracejadas correspondem ao ajuste através do método dos mínimos quadrados; linhas pontilhadas representam o ajuste pelo método da mínima mediana e a linha cheia corresponde ao ajuste determinado pelo algoritmo de PROGRESS. Em cada gráfico está indicado o valor da diferença entre o gradiente determinado pelo método dos mínimos quadrados e o determinado pelo algoritmo de PROGRESS ( $\Delta G \equiv G($MQ$) - G($PRO$)$). Nota-se que, para NGC 2613, o método clássico é perturbado pela última medida de (B-V). Para esta galáxia, e para UGC 3973, os diferentes métodos atribuem valores substancialmente diferentes para os gradientes.

Figure: Gradientes de cor (B-V) e (U-B) para as galáxias de nossa amostra em função do excesso de cor E(B-V) provocado pela extinção Galáctica (painéis superiores), e em função da inclinação da galáxia, representada aqui pelo parâmetro $R_{25}$ do RC3 (painéis inferiores). A ausência de correlações indica que as extinções Galáctica e intrínseca não interferem na determinação dos gradientes de cor.

Os dados em LdV83,85 não estão corrigidos de fatores externos, tais como averme-lhamento Galáctico e avermelhamento intrínseco, mas somente de fatores observacionais e da extinção atmosférica. Na determinação dos gradientes de cor, a correção por averme-lhamento Galáctico não é necessária, já que somente provocaria um deslocamento vertical do gradiente, não afetando sua inclinação, pois a mesma correção é aplicada para toda a galáxia. Isto porque o excesso de cor produzido pela extinção Galáctica pode ser expresso como função somente das coordenadas galácticas do objeto⁶. A correção pelo avermelhamento intrínseco é difícil de prever corretamente, devido aos problemas de inclinação das galáxias e da questão da espessura óptica de galáxias espirais (e.g., Giovanelli et al. 1994,1995; de Jong 1996c). De qualquer maneira, tal correção acarretaria modificações sem importância nos gradientes de cor, tendo em vista as incertezas envolvidas. 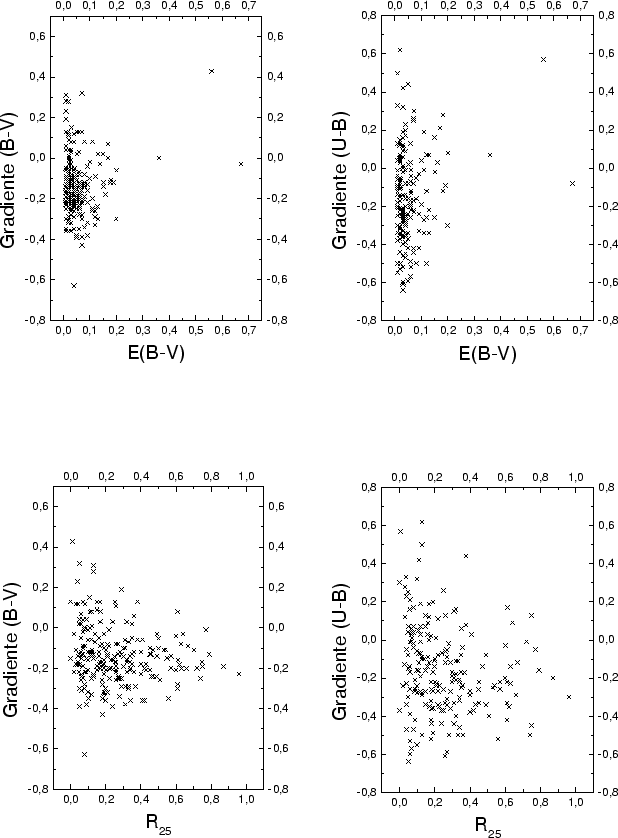De fato, a Figura 2.5 mostra que os avermelhamentos Galáctico e intrínseco não interferem na determinação dos gradientes de cor. Os painéis superiores desta figura mostram que não há qualquer correlação entre os gradientes que determinamos e o avermelhamento Galáctico, representado pelo excesso de cor $E(B-V)$. Por outro lado, como a extinção intrínseca varia com a inclinação do disco da galáxia em relação à nossa linha de visada, elaboramos os painéis inferiores da figura, que exibem os gradientes em função do parâmetro $R_{25}$ do RC3, que representa a inclinação da galáxia. Nestes painéis, as galáxias cujos discos encontram-se mais inclinados em relação à nossa linha de visada, portanto vistos de perfil, são as que possuem valores maiores de $R_{25}$. A ausência de correlações indica que o avermelhamento intrínseco não interfere na determinação dos gradientes. No entanto, essas extinções produzem efeitos bastante consideráveis nos índices de cor. Voltaremos a tratar deste assunto na próxima seção.

Footnotes

... objeto⁶

Na verdade, se a cor varia ao longo da galáxia, o fato da extinção pela poeira interestelar variar com o comprimento de onda da luz faz com que a correção pelo avermelhamento seja distinta ao longo da galáxia. No entanto, estamos desprezando este efeito, considerando que este somente produz perturbações muito pequenas em comparação com os erros fotométricos e na determinação dos gradientes.