 |
Para certificar-nos que o nosso código determina de forma confiável os parâmetros estruturais de bojos e discos em galáxias, realizamos uma série de testes em 41 galáxias artificiais. As imagens das galáxias artificiais foram sintetizadas de forma que conhecemos seus parâmetros estruturais verdadeiros, podendo assim compará-los com os obtidos pelo BUDDA. O código foi aplicado como em galáxias reais, exceto que foi aplicado apenas 1 vez por galáxia, e apenas em alguns casos as elipticidades e os ângulos de posição foram tratados como em galáxias reais (ver subseção anterior). Isto significa que os resultados dos testes são de fato um limite inferior para a precisão do código.
As estimativas iniciais dos parâmetros foram escolhidas aleatoriamente, sendo bastante distintas dos valores verdadeiros em muitos casos. No entanto, o código mostrou-se bastante robusto, já que, não importando quão distante do valor verdadeiro a estimativa inicial de um certo parâmetro for, o BUDDA gradualmente converge para o valor correto, dentro da margem de erro. Uma contribuição de erro Poissônico foi adicionada em algumas das imagens sintéticas, e constatamos que essa é uma fonte menor de erro, desde que a razão sinal/ruído seja razoável (i.e., da ordem de 50 nas regiões centrais da galáxia).
Dois tipos de testes foram realizados. No primeiro, imagens de boa resolução espacial foram simuladas. Nestes testes, adotamos um ``seeing'' de 2'' e uma galáxia observada com eixo maior igual a 1'. Este é um valor típico para a maior parte das observações de galáxias em telescópios terrestres sem óptica ativa ou adaptativa. Os resultados desta Tese, no entanto, são baseados em imagens com qualidade superior, em média. Para checar como o BUDDA se comporta em condições inferiores, por exemplo, no estudo de galáxias anãs, ou de galáxias em ``redshifts'' intermediários, fizemos testes nos quais a qualidade de imagem é duas vezes mais pobre.
 |
 |
 |
 |
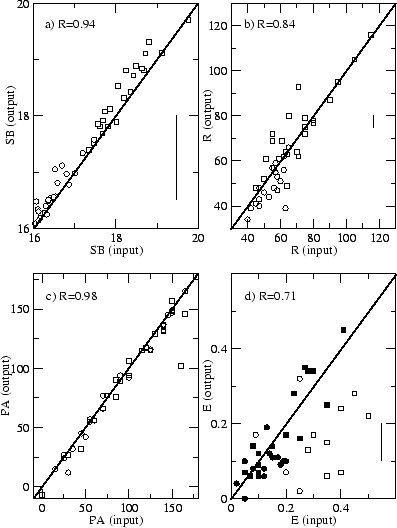
Os resultados dos testes estão nas Fig(s). 4.1 e 4.2, para os casos de boa resolução, e nas
Fig(s). 4.3 e 4.4, para os casos de baixa resolução espacial. Na Fig. 4.1 vê-se que a confiabilidade do
código é excelente na determinação dos brilhos superficiais, escalas de comprimento e ângulos de
posição de bojos e discos. Embora haja algumas tendências menores o acordo está sempre dentro da
margem de erro. Em particular, na Fig. 4.1, no brilho superficial central dos discos determinado pelo
nosso algoritmo parece estar embutido um erro sistemático de cerca de 0.10 mag. No entanto,
este efeito pode ser apenas uma flutuação estatística, já que, por exemplo, não
aparece na Fig. 4.3. De todo modo, não é um efeito significativo e preocupante.
As elipticidades de bojos e discos são, no entanto, sujeitas a erros maiores. A razão
para isto vem do fato de que, para as baixas elipticidades, típicas das galáxias que consideramos nesta
Tese, para uma elipticidade fixa, é sempre possível encontrar um outro conjunto de parâmetros que resulta
em um erro final não muito distinto daquele para a solução ótima. O erro final é relativamente
insensível ao valor das elipticidades. A situação se agrava, por exemplo, se a razão B/D é maior do que
1 (o que é verdadeiro para a maior parte das nossas galáxias),
já que neste caso uma variação na elipticidade do disco praticamente
não tem impacto no cálculo do erro final. O mesmo pode ocorrer com o ângulo de posição se a elipticidade for
muito baixa. Assim, é necessário cuidado na interpretação dos resultados dos testes
com relação à elipticidade. A elipticidade dos bojos mais excêntricos é algumas vezes sub-estimada, mas ainda
dentro dos erros. Na análise de galáxias reais, a questão da elipticidade é fácil de ser tratada eficientemente.
Basta tomar as precauções discutidas na subseção anterior, isto é: encontrar as elipticidades e os ângulos de
posição via outros modos (e.g., tarefa ELLIPSE do IRAF); aplicar o código pela primeira vez com estes
valores fixos; e finalmente aplicar o código mais uma vez, deixando estes parâmetros livres, e utilizando os
resultados da primeira aplicação como estimativa inicial na segunda aplicação. Os símbolos sólidos
nas Fig(s). 4.1(d) e 4.3(d) mostram como o BUDDA determina de maneira confiável as elipticidades
quando estas são tratadas como em galáxias reais. O coeficiente de correlação de Pearson R
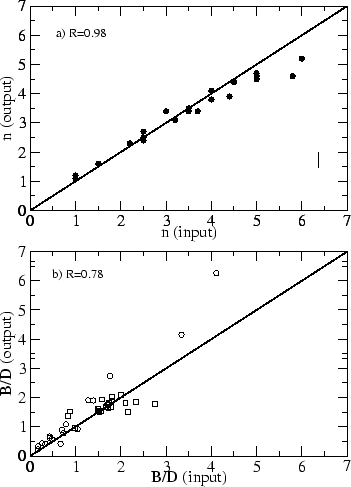
indicado nestes casos se refere apenas aos símbolos sólidos. Na Fig. 4.2 apresentamos os resultados
referentes aos índices de Sérsic e às razões B/D. Mais uma vez os testes mostram que os resultados
do algoritmo são excelentes. Para valores altos de ![]() , o ``seeing'' adotado pode implicar em uma
sub-estimativa; porém, para a maior parte dos bojos, que tem
, o ``seeing'' adotado pode implicar em uma
sub-estimativa; porém, para a maior parte dos bojos, que tem ![]() , este efeito não é importante.
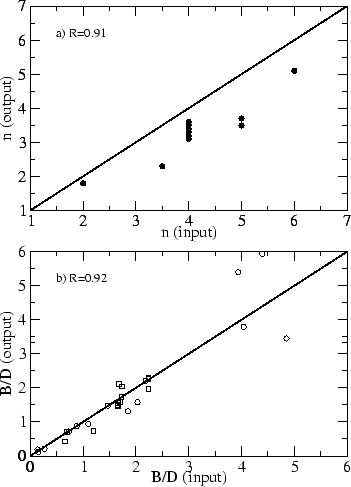
Para condições de baixa resolução espacial, o resultado dos testes nas Fig(s). 4.3 e 4.4 também é
muito encorajador.
, este efeito não é importante.
Para condições de baixa resolução espacial, o resultado dos testes nas Fig(s). 4.3 e 4.4 também é
muito encorajador.
 |
 |
Para verificar qual é a influência dos erros nas imagens residuais, essas foram simuladas para o caso de galáxias sintéticas também. Ou seja, de uma imagem original de uma galáxia artificial, subtraíu-se o modelo completo obtido com o BUDDA. Na Fig. 4.5 mostramos um caso de boa resolução espacial, e na Fig. 4.6 um caso de resolução pobre. Essas figuras mostram que a discrepância se restringe à região central, que tem um tamanho da ordem do ``seeing''. A Fig. 4.6 apresenta o caso de um ajuste propositadamente pobre, em particular, com relação aos ângulos de posição e às elipticidades, mostrando que um problema como este pode ser facilmente identificado pelo padrão bipolar que aparece. A galáxia sintética original ocupa toda a imagem, e os níveis de brilho e contraste foram ajustados de modo a reforçar as diferenças.
Outro ponto relevante que aparece nestes testes é a sensibilidade do código em identificar discos que são até 6 vezes menos luminosos que seus respectivos bojos, embora este valor dependa das diferenças nas propriedades geométricas destas componentes. De fato, os resultados dos testes com galáxias reais (próxima subseção) mostram que o código poder ser ainda mais sensível. De todo modo, este resultado reforça a descoberta de Gadotti & de Souza (2003a, b), feita com o BUDDA, da ausência de um disco substancial nas galáxias de tipo SB0 NGC 4608 e NGC 5701 (ver adiante), já que a razão B/D em luminosidade em S0's normais é da ordem de 2 (BM98).
Como foi notado acima, os erros determinados pelo algoritmo podem às vezes estar super-estimados.
Isto parece ser especialmente verdadeiro para o brilho superficial e o ângulo de posição. Os erros
(1![]() ) para o brilho superficial são tipicamente cerca de
0.75 mag arcsec
) para o brilho superficial são tipicamente cerca de
0.75 mag arcsec![]() . No entanto, nas Fig(s). 4.1 e 4.3,
vê-se que a diferenca entre o brilho superficial verdadeiro e aquele determinado pelo código está
tipicamente dentro de uma faixa de 0.25 mag arcsec
. No entanto, nas Fig(s). 4.1 e 4.3,
vê-se que a diferenca entre o brilho superficial verdadeiro e aquele determinado pelo código está
tipicamente dentro de uma faixa de 0.25 mag arcsec![]() .
Nestas figuras, não há barras de erro nos ângulos de posição
porque na maior parte das vezes o código tem dificuldades em estimar o erro neste parâmetro. Este fato está
relacionado com a questão da elipticidade discutida acima. Também não há barras de erro nas razões
B/D (Fig(s). 4.2 e 4.4) porque estas são calculadas diretamente dos modelos.
.
Nestas figuras, não há barras de erro nos ângulos de posição
porque na maior parte das vezes o código tem dificuldades em estimar o erro neste parâmetro. Este fato está
relacionado com a questão da elipticidade discutida acima. Também não há barras de erro nas razões
B/D (Fig(s). 4.2 e 4.4) porque estas são calculadas diretamente dos modelos.