Grande parte do sucesso de um experimento numérico decorre do correto
estabelecimento das condições iniciais do problema. Em geral, os códigos se utilizam
de unidades viriais, que facilitam a confecção do algoritmo. Nestas unidades,
![]() , onde
, onde ![]() e
e ![]() são, respectivamente, a massa total e a energia total
do sistema. Nestas unidades, as novas unidades físicas são, para massa, comprimento
e tempo, respectivamente:
são, respectivamente, a massa total e a energia total
do sistema. Nestas unidades, as novas unidades físicas são, para massa, comprimento
e tempo, respectivamente:
![$\displaystyle {[l]}={-\frac{GM^2}{4E}},$](img459.png) |
(83) | ||
![$\displaystyle {[t]}={\frac{GM^{5/2}}{(-4E)^{3/2}}}.$](img460.png) |
Veremos adiante que as nossas simulações utilizam um código hierárquico, com discos exponenciais e esferas de Plummer. No caso do disco exponencial, a energia total do sistema é dada por (BT87):
| (84) |
onde ![]() é o raio característico do disco e
é o raio característico do disco e
![]() é a
densidade superficial central do disco. Assim, tomando, por exemplo,
é a
densidade superficial central do disco. Assim, tomando, por exemplo,
![]() M
M![]() e
e ![]() Kpc, valores representativos para o disco
da Galáxia, temos:
Kpc, valores representativos para o disco
da Galáxia, temos:
| (85) | |||
É fácil verificar que, então, as unidades para velocidade e velocidade angular são,
respectivamente, 207 Km/s e 35 Km s![]() Kpc
Kpc![]() .
.
Para a esfera de Plummer (Aarseth, Hénon & Wielen 1974),
 |
(86) |
onde ![]() é o raio característico da esfera. Se
é o raio característico da esfera. Se
![]() M
M![]() e
e ![]() Kpc, valores típicos para os bojos de galáxias
lenticulares (ver adiante), teremos:
Kpc, valores típicos para os bojos de galáxias
lenticulares (ver adiante), teremos:
| (87) | |||
O raio efetivo (i.e., aquele que contém metade da massa) na esfera de Plummer é igual
a 1.31![]() (Evstigneeva, Reshetnikov & Sotnikova 2002). Note que utilizamos a Eq. (3.56) para
definir as unidades apenas nas simulações em que não há uma esfera de Plummer. No restante
das simulações, as unidades foram estabelecidas através das propriedades da esfera de Plummer.
(Evstigneeva, Reshetnikov & Sotnikova 2002). Note que utilizamos a Eq. (3.56) para
definir as unidades apenas nas simulações em que não há uma esfera de Plummer. No restante
das simulações, as unidades foram estabelecidas através das propriedades da esfera de Plummer.
Durante a evolução do sistema, o passo de tempo a ser utilizado deve ser tal que haja muitos
passos por tempo de cruzamento, de modo a maximizar a precisão dos resultados.
Em nossas simulações, utilizamos um passo de tempo
fixo tipicamente igual a ![]() anos, o que dá
cerca de 10
anos, o que dá
cerca de 10![]() passos por
passos por ![]() para as galáxias que estaremos simulando.
O parâmetro de suavização sugerido por Merritt (1996) para
para as galáxias que estaremos simulando.
O parâmetro de suavização sugerido por Merritt (1996) para ![]() , que é o número de partículas
que comumente utilizamos em nossas simulações, está na faixa de 0.01 a 0.05. Tipicamente, adotamos
um valor para o parâmetro de suavização de 0.05. Porém, este valor foi algumas vezes modificado
para 0.08, 0.1, 0.25 e 0.5, de forma a podermos avaliar o impacto da suavização nos resultados das
simulações (isto será discutido adiante). Em geral, nas simulações de galáxias,
, que é o número de partículas
que comumente utilizamos em nossas simulações, está na faixa de 0.01 a 0.05. Tipicamente, adotamos
um valor para o parâmetro de suavização de 0.05. Porém, este valor foi algumas vezes modificado
para 0.08, 0.1, 0.25 e 0.5, de forma a podermos avaliar o impacto da suavização nos resultados das
simulações (isto será discutido adiante). Em geral, nas simulações de galáxias,
![]() varia também nesta faixa de valores. Note que, fisicamente, isto implica em um valor
para o parâmetro de suavização de algumas centenas de parsecs. O ângulo de abertura que utilizamos foi
varia também nesta faixa de valores. Note que, fisicamente, isto implica em um valor
para o parâmetro de suavização de algumas centenas de parsecs. O ângulo de abertura que utilizamos foi
![]() , que é o que melhor atinge o compromisso entre precisão e tempo de cálculo, e
é também tipicamente utilizado por outros pesquisadores.
, que é o que melhor atinge o compromisso entre precisão e tempo de cálculo, e
é também tipicamente utilizado por outros pesquisadores.
Nas simulações que serão apresentadas nas próximas seções, utilizamos uma esfera de Plummer
para descrever o bojo, que segue a seguinte expressão para a densidade de massa ![]() em função
da distância galactocêntrica
em função
da distância galactocêntrica ![]() :
:
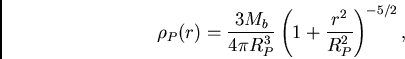 |
(88) |
o que corresponde a um potencial (ver, e.g., BT87)
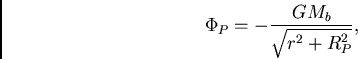 |
(89) |
onde ![]() é a massa total do bojo.
é a massa total do bojo.
O disco é descrito por um perfil exponencial (Freeman 1970, 1978; van de Kruit & Searle 1981):
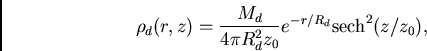 |
(90) |
cujo potencial corresponde a (em uma aproximação para disco fino)
![\begin{displaymath}
\Phi_d(r,z)=-GM_d\int_0^\infty\frac{J_0(kr)e^{-k\vert z\vert}}{[1+(kR_d)^2]^{\frac{3}{2}}}{\rm d}k,
\end{displaymath}](img485.png) |
(91) |
onde ![]() é a função de Bessel cilíndrica de ordem 0,
é a função de Bessel cilíndrica de ordem 0, ![]() é uma constante,
é uma constante,
![]() é a massa do disco, e
é a massa do disco, e ![]() é a sua escala de altura. Desta forma, o disco é
isotérmico com escala de altura constante. Neste caso, o parâmetro
é a sua escala de altura. Desta forma, o disco é
isotérmico com escala de altura constante. Neste caso, o parâmetro ![]() de Toomre, que
estabelece se disco é instável à formação de uma barra, fica definido pela Eq. (1.1) e é,
portanto, proporcional à dispersão de velocidades das estrelas na direção radial,
de Toomre, que
estabelece se disco é instável à formação de uma barra, fica definido pela Eq. (1.1) e é,
portanto, proporcional à dispersão de velocidades das estrelas na direção radial, ![]() .
Esta, por sua vez, fica definida pela dispersão na direção vertical
.
Esta, por sua vez, fica definida pela dispersão na direção vertical ![]() , já que temos
, já que temos
![]() . E, finalmente, é a escala de altura do disco que define
. E, finalmente, é a escala de altura do disco que define ![]() , através
da relação
, através
da relação
![]() , onde
, onde ![]() é a densidade superficial projetada de
massa do disco (ver, e.g., van der Kruit 2002). Assim, em última instância,
é a densidade superficial projetada de
massa do disco (ver, e.g., van der Kruit 2002). Assim, em última instância, ![]() é determinado
por
é determinado
por ![]() , e varia ao longo do raio do disco. Além disso, a dispersão
na direção azimutal é dada por
, e varia ao longo do raio do disco. Além disso, a dispersão
na direção azimutal é dada por
![]() , onde
, onde ![]() é a
freqüência de epiciclo e
é a
freqüência de epiciclo e ![]() é a velocidade angular de rotação das estrelas (e.g., Teuben 1995).
é a velocidade angular de rotação das estrelas (e.g., Teuben 1995).
Entretanto, veremos que é possível inicializar os experimentos numéricos atribuindo um valor fixo
para ![]() . Desta forma, o caminho é inverso, e
. Desta forma, o caminho é inverso, e
![]() fica definido por
fica definido por ![]() , e estabelece
, e estabelece
![]() ,
, ![]() e
e ![]() .
Alguns dos experimentos foram realizados desta forma, de modo a forçar a instabilidade de barra, que,
de outro modo, não ocorre em discos construídos com a finalidade de reproduzir os discos observados
em galáxias lenticulares. Mais detalhes acerca deste aspecto serão discutidos adiante, mas note que,
assim, o disco deixa de ser isotérmico e com
.
Alguns dos experimentos foram realizados desta forma, de modo a forçar a instabilidade de barra, que,
de outro modo, não ocorre em discos construídos com a finalidade de reproduzir os discos observados
em galáxias lenticulares. Mais detalhes acerca deste aspecto serão discutidos adiante, mas note que,
assim, o disco deixa de ser isotérmico e com ![]() constante (Teuben 1995). O fato de o disco ser isotérmico significa
que
constante (Teuben 1995). O fato de o disco ser isotérmico significa
que ![]() é independente de
é independente de ![]() (ver van der Kruit 1981).
(ver van der Kruit 1981).
Na maior parte dos experimentos realizados (em particular, todos aqueles na Tab. 3.1),
foi feita uma correção no disco para o
fluxo assimétrico (``asymmetric drift''; ver BT87; BM98). Isto permite representar mais
adequadamente o comportamento cinemáti-co das estrelas em um disco real. O fluxo assimétrico
é a tendência observada de que estrelas com valores mais elevados na dispersão de velocidades
têm um valor reduzido para a velocidade circular de rotação, ![]() , que é a velocidade que uma
dada estrela teria se assumirmos que sua órbita é perfeitamente circular. Ninkovic (1992) mostra que
o fluxo assimétrico pode ser parametrizado como
, que é a velocidade que uma
dada estrela teria se assumirmos que sua órbita é perfeitamente circular. Ninkovic (1992) mostra que
o fluxo assimétrico pode ser parametrizado como
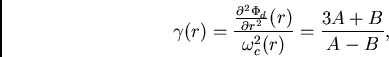 |
(92) |
onde ![]() é a velocidade circular angular, e
é a velocidade circular angular, e ![]() e
e ![]() são as constantes de Oort,
dadas por
são as constantes de Oort,
dadas por
 |
(93) |
e
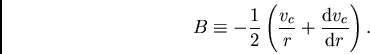 |
(94) |
Observações na vizinhança solar20indicam que
![]() (ver também Mihalas & Binney 1981; Dehnen & Binney 1998). Esta correção
pode parecer, à primeira vista, preciosista. Entretanto, dado que a dispersão de velocidades é um
parâmetro físico fundamental no que se refere à formação e evolução de barras, é de extrema
importância neste estudo.
(ver também Mihalas & Binney 1981; Dehnen & Binney 1998). Esta correção
pode parecer, à primeira vista, preciosista. Entretanto, dado que a dispersão de velocidades é um
parâmetro físico fundamental no que se refere à formação e evolução de barras, é de extrema
importância neste estudo.
Para descrever o halo de matéria escura em nossas simulações, não utilizamos partículas, mas apenas um potencial fixo. Portanto, o halo em nossos experimentos é rígido, e segue um potencial logarítmico, dado por
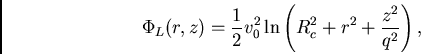 |
(95) |
cuja distribuição de densidade correspondente é dada por
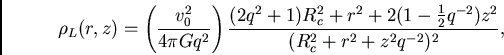 |
(96) |
onde ![]() é a velocidade assimptótica na curva de rotação da galáxia simulada, devido à presença do
halo,
é a velocidade assimptótica na curva de rotação da galáxia simulada, devido à presença do
halo, ![]() é o raio do caroço central do halo, no qual a variação de densidade é reduzida, e
é o raio do caroço central do halo, no qual a variação de densidade é reduzida, e ![]() é a asfericidade na
direção vertical (
é a asfericidade na
direção vertical (![]() , onde
, onde ![]() ,
, ![]() e
e ![]() são os semi-eixos do halo, com
são os semi-eixos do halo, com ![]() ). Note que também é
possível impôr a condição de que
). Note que também é
possível impôr a condição de que ![]() , i.e., o halo pode não ser circular também no plano do disco da galáxia.
Assim, o halo pode ser esférico (
, i.e., o halo pode não ser circular também no plano do disco da galáxia.
Assim, o halo pode ser esférico (![]() ), prolato (
), prolato (![]() ), oblato (
), oblato (![]() ) ou triaxial (
) ou triaxial (![]() ).
A massa contida no caroço do halo é dada por
).
A massa contida no caroço do halo é dada por
![]() , já em unidade viriais.
, já em unidade viriais.