A realização dos experimentos numéricos desta seção teve o intuito de verificar as condições para
a formação de barras em discos de galáxias, além de estimar parâmetros físicos relacionados à formação e
evolução destas barras. Com estes experimentos, pode-se avaliar, por exemplo, as escalas de tempo para
a formação e o espessamento vertical das barras, bem como verificar quantitativamente o aumento na dispersão
de velocidades na direção vertical, ![]() , que ocorre durante a evolução da barra. Outros aspectos
interessantes deste problema, que podem ser agora abordados, são a evolução do comprimento
, que ocorre durante a evolução da barra. Outros aspectos
interessantes deste problema, que podem ser agora abordados, são a evolução do comprimento ![]() da
barra e a sua velocidade angular
da
barra e a sua velocidade angular ![]() . Os valores destes e de outros parâmetros podem ser
comparados com as observações nos Capítulos 2 e 4.
. Os valores destes e de outros parâmetros podem ser
comparados com as observações nos Capítulos 2 e 4.
Para realizar estas simulações ![]() -corpos, utilizamos o pacote NEMO (Teuben 1995; ver
http://bima.astro.umd.edu/nemo/) e as condições iniciais expostas na seção anterior. O código de cálculo
de forças é baseado em um algoritmo hierárquico intensamente utilizado na literatura (Barnes & Hut 1986).
-corpos, utilizamos o pacote NEMO (Teuben 1995; ver
http://bima.astro.umd.edu/nemo/) e as condições iniciais expostas na seção anterior. O código de cálculo
de forças é baseado em um algoritmo hierárquico intensamente utilizado na literatura (Barnes & Hut 1986).
Os discos das galáxias foram construídos através da tarefa MKEXPDISK, e os bojos através da tarefa MKPLUMMER. A soma destas componentes se dá via a tarefa SNAPSTACK, que compõe o sistema inicial completo. Nas simulações em que não há um halo de matéria escura, a tarefa HACKCODE1 foi utilizada para a evolução do sistema; a introdução de um halo escuro rígido, descrito pelo potencial LOG, foi realizada com a tarefa HACKCODE3.
Como nossos objetivos incluem também avaliar diferenças na evolução das propriedades de barras em
galáxias de tipos morfológicos
distintos, realizamos uma extensa pesquisa na literatura em busca dos parâmetros necessários para
melhor descrever estes sistemas. Em primeiro lugar, Roberts & Haynes (1994) mostram que valores característicos
para a massa total e raio de galáxias (na isofota de 25 ![]() mag arcsec
mag arcsec![]() ),
com tipos morfológicos desde S0's até Sc's, é, respectivamente,
da ordem de
),
com tipos morfológicos desde S0's até Sc's, é, respectivamente,
da ordem de ![]() M
M![]() e 10 a 20 Kpc. Isto sem uma variação sistemática muito significativa
ao longo destas classes morfológicas, principalmente considerando o amplo espalhamento destes
parâmetros em cada classe. Por outro lado, a razão entre as luminosidades de bojo e disco variam
sistematicamente: tipicamente 1.85 para S0's, 1 para Sa's, 1/3 para Sb's, e apenas 0.18 para Sc's (BM98).
Além disso, a massa do disco da Galáxia é estimada em
e 10 a 20 Kpc. Isto sem uma variação sistemática muito significativa
ao longo destas classes morfológicas, principalmente considerando o amplo espalhamento destes
parâmetros em cada classe. Por outro lado, a razão entre as luminosidades de bojo e disco variam
sistematicamente: tipicamente 1.85 para S0's, 1 para Sa's, 1/3 para Sb's, e apenas 0.18 para Sc's (BM98).
Além disso, a massa do disco da Galáxia é estimada em
![]() M
M![]() , o que nos permite
assumir uma massa para o bojo da Via Láctea de aproximadamente
, o que nos permite
assumir uma massa para o bojo da Via Láctea de aproximadamente
![]() M
M![]() , se
assumimos uma razão massa/luminosidade da ordem de 5 M
, se
assumimos uma razão massa/luminosidade da ordem de 5 M
![]() na banda
na banda ![]() , e que
o tipo morfológico da Galáxia é Sbc
(ver BT87). Com estes dados podemos estabelecer valores característicos para a massa dos bojos e discos
em nossas simulações, bem como a dimensão (semi-eixo maior) dos discos das galáxias.
, e que
o tipo morfológico da Galáxia é Sbc
(ver BT87). Com estes dados podemos estabelecer valores característicos para a massa dos bojos e discos
em nossas simulações, bem como a dimensão (semi-eixo maior) dos discos das galáxias.
Porém, ainda é necessário estabelecer muitos outros parâmetros. Vejamos quais são os valores típicos
para as escalas de comprimento. Para o disco da Galáxia, ![]() vale 3.5
vale 3.5![]() 0.5 Kpc (BT87).
Através da análise estrutural de galáxias com imagens na banda
0.5 Kpc (BT87).
Através da análise estrutural de galáxias com imagens na banda ![]() , de Jong (1996c) encontra valores para
, de Jong (1996c) encontra valores para ![]() de
2 a 5 Kpc, enquanto Kent (1985) encontra valores de 1 a 10 Kpc em uma análise semelhante na banda
de
2 a 5 Kpc, enquanto Kent (1985) encontra valores de 1 a 10 Kpc em uma análise semelhante na banda ![]() .
Para o raio efetivo dos bojos, os valores determinados por de Jong são tipicamente de 0.2 a 0.7 Kpc, e os de
Kent 0.5 a 5 Kpc. Note que encontramos valores semelhantes na análise estrutural do Capítulo 4 (ver
também Apêndice A). Também é importante notar que o espalhamento destes parâmetros é, da
mesma forma como para outros parâmetros, bastante elevado,
e que não há uma variação sistemática bem definida ao longo das diferentes
classes morfológicas, desde S0's a Sc's. A escala de altura dos discos pode ser baseada também nos valores para
a Via Láctea. Para estrelas jovens, de tipo espectral O a B,
.
Para o raio efetivo dos bojos, os valores determinados por de Jong são tipicamente de 0.2 a 0.7 Kpc, e os de
Kent 0.5 a 5 Kpc. Note que encontramos valores semelhantes na análise estrutural do Capítulo 4 (ver
também Apêndice A). Também é importante notar que o espalhamento destes parâmetros é, da
mesma forma como para outros parâmetros, bastante elevado,
e que não há uma variação sistemática bem definida ao longo das diferentes
classes morfológicas, desde S0's a Sc's. A escala de altura dos discos pode ser baseada também nos valores para
a Via Láctea. Para estrelas jovens, de tipo espectral O a B, ![]() vale cerca de 200 pc, enquanto que,
para estrelas de tipo G,
vale cerca de 200 pc, enquanto que,
para estrelas de tipo G, ![]() é igual a cerca de 700 pc (Bahcall & Soneira 1980; BT87). A dimensão (semi-eixo maior)
dos bojos é estimada em aproximadamente 5 Kpc para S0's, 4 Kpc para Sa's, e 1 a 2 Kpc para Sc's (BM98).
é igual a cerca de 700 pc (Bahcall & Soneira 1980; BT87). A dimensão (semi-eixo maior)
dos bojos é estimada em aproximadamente 5 Kpc para S0's, 4 Kpc para Sa's, e 1 a 2 Kpc para Sc's (BM98).
Com relação aos parâmetros dos halos, sabemos que a velocidade assimptótica de rotação nos discos
de galáxias tem valores típicos da ordem de 300 Km/s em S0's a 200 Km/s em Sc's (Rubin et al. 1985;
Persic & Salucci 1995; ver também Fig. 1.5). Além disso, Begeman, Broeils & Sanders (1991) estimam
valores para o raio do caroço, ![]() , entre 2 a 10 Kpc.
, entre 2 a 10 Kpc.
Com este levantamento dos parâmetros estruturais observados para as componentes bojo, disco e halo de galáxias, pudemos estabelecer adequadamente as condições iniciais para os experimentos que representam galáxias de classe morfológica desde S0/a a Sbc. Na Tab. 3.1, exibimos os parâmetros que definem as condições iniciais do sistema para uma seleção dos experimentos realizados mais relevantes. Note que uma longa série inicial de experimentos foi realizada com o intuito de identificar os detalhes envolvidos na preparação destes, bem como conhecer melhor o próprio pacote NEMO. As simulações têm duração tipicamente de 2 a 3 Gano, o que consumiu, em média, cerca de 140 horas de tempo de processamento por experimento. Foi utilizado um PC com processador Pentium de 1 GHz e 1 Gbyte de memória.
A variação da energia total ao fim dos experimentos foi tipicamente da ordem de 0.3%, com variações similares na posição do centro de massa, de forma que isso mostra que o passo de tempo e o ângulo de abertura foram bem estabelecidos e os resultados são robustos.
| Exp. | |
|
|
|
|
|
|
|
|
|
|
|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) |
| 9 | 1.5
|
0.38 | 2 | 6
|
3.5 | 350 | 10 | 8 | 220 | 4.4
|
... | 0.05 |
| 10 | 1.5
|
0.38 | 2 | 6
|
3.5 | 200 | 10 | 8 | 220 | 4.4
|
... | 0.05 |
| 11 | 1.5
|
0.38 | 2 | 6
|
3.5 | 350 | 10 | ... | ... | ... | ... | 0.05 |
| 12 | 1.5
|
0.38 | 2 | 6
|
3.5 | 200 | 10 | ... | ... | ... | ... | 0.05 |
| 13 | ... | ... | ... | 6
|
3.5 | 350 | 10 | ... | ... | ... | ... | 0.05 |
| 14 | ... | ... | ... | 6
|
3.5 | 450 | 10 | ... | ... | ... | ... | 0.05 |
| 15 | 1.5
|
0.38 | 2 | 6
|
3.5 | 200 | 10 | 8 | 220 | 4.4
|
0.5 | 0.05 |
| 16 | 1.5
|
0.38 | 2 | 6
|
3.5 | 450 | 10 | 8 | 220 | 4.4
|
0.5 | 0.05 |
| 17 | 1.5
|
0.38 | 2 | 6
|
3.5 | 450 | 10 | 8 | 220 | 4.4
|
0.1 | 0.05 |
| 18 | 1.5
|
0.38 | 2 | 6
|
3.5 | 350 | 10 | 8 | 220 | 4.4
|
0.5 | 0.05 |
| 19 | 1.5
|
0.38 | 2 | 6
|
3.5 | 350 | 10 | 8 | 220 | 4.4
|
0.1 | 0.05 |
| 20 | 1.5
|
0.38 | 2 | 6
|
3.5 | 450 | 10 | ... | ... | ... | 0.1 | 0.05 |
| 21 | 1.5
|
0.38 | 2 | 6
|
3.5 | 450 | 10 | ... | ... | ... | 0.5 | 0.05 |
| 22 | ... | ... | ... | 6
|
3.5 | 450 | 10 | ... | ... | ... | 0.5 | 0.05 |
| 23 | 1.5
|
0.38 | 2 | 6
|
5 | 450 | 13 | 8 | 220 | 4.4
|
0.1 | 0.05 |
| 24 | 1.5
|
0.38 | 2 | 6
|
3.5 | 450 | 10 | 8 | 220 | 4.4
|
0.25 | 0.05 |
| 25 | 1.5
|
0.38 | 2 | 6
|
3.5 | 450 | 10 | 8 | 220 | 4.4
|
0.25 | 0.25 |
| 26 | 1.5
|
0.38 | 2 | 6
|
3.5 | 450 | 10 | 8 | 220 | 4.4
|
0.25 | 0.5 |
| 27 | 5 |
0.38 | 1 | 1
|
3.5 | 450 | 12 | 8 | 220 | 4.4
|
0.25 | 0.25 |
| 28 | 5 |
0.76 | 3 | 1
|
3.5 | 450 | 12 | 8 | 220 | 4.4
|
0.25 | 0.25 |
| 30 | 1.5
|
2.29 | 5 | 1
|
6 | 450 | 12 | 8 | 300 | 8
|
0.25 | 0.08 |
| 33 | 1
|
1.53 | 4 | 2
|
4 | 450 | 12 | 8 | 280 | 7
|
0.25 | 0.25 |
| 34 | 1.5
|
2.29 | 5 | 1
|
6 | 450 | 12 | 8 | 300 | 8
|
0.25 | 0.25 |
Inspecionando a Tab 3.1, nota-se que as propriedades dos sistemas investigados fazem com que as simulações de números 9 a 26 sejam representativas de galáxias com tipo morfológico Sbc (exceto, evidentemente, aqueles experimentos que foram realizados sem bojo e/ou halo, com o intuito de verificar a influência destas componentes na estabilidade do disco). Os experimentos no(s). 27 e 28 são representativos de galáxias de tipo Scd; o experimento no. 33 se refere a uma galáxia de tipo Sab, e os de no(s). 30 e 34 a uma S0/a.
Vejamos, agora, os resultados mais relevantes que pudemos obter a partir destes experimentos. Antes de tudo, através
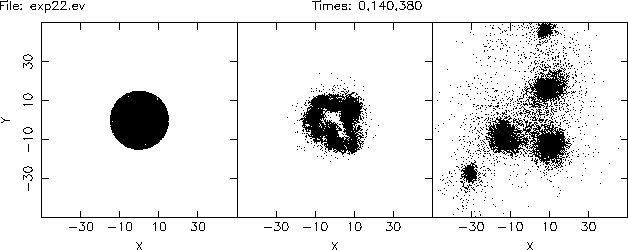
de simulações que incluem apenas um disco, como as de no(s). 13 e 14, por exemplo, verificamos que, se o valor para
![]() é da ordem de apenas 200 pc, ocorre a fragmentação do disco. Isto porque, como vimos, o valor para o
parâmetro de Toomre
é da ordem de apenas 200 pc, ocorre a fragmentação do disco. Isto porque, como vimos, o valor para o
parâmetro de Toomre ![]() depende da escala de altura do disco. Este resultado mostra que quando esta escala
é da ordem de 200 pc, ou menor, instabilidades locais dominam o disco, e este se fragmenta em condensações individuais
(Fig. 3.2).
Note que isto ocorre rapidamente, em escalas de tempo menores do que a escala de tempo dinâmica21do sistema, que é da ordem de 10
depende da escala de altura do disco. Este resultado mostra que quando esta escala
é da ordem de 200 pc, ou menor, instabilidades locais dominam o disco, e este se fragmenta em condensações individuais
(Fig. 3.2).
Note que isto ocorre rapidamente, em escalas de tempo menores do que a escala de tempo dinâmica21do sistema, que é da ordem de 10![]() anos.
Nestes sistemas de discos puros e com baixas escalas de altura (i.e, excessivamente finos), também verificamos que,
para algumas das condensações individuais, a dispersão de velocidades vertical,
anos.
Nestes sistemas de discos puros e com baixas escalas de altura (i.e, excessivamente finos), também verificamos que,
para algumas das condensações individuais, a dispersão de velocidades vertical, ![]() , alcança valores
muito elevados e não realísticos. De fato, estas condensações acabam por separar-se do disco e se dissolvem.
Este fenômeno parece estar relacionado com o efeito ``hose'' (ver, e.g., Seção 1.2), já que este efeito é
favorecido para valores iniciais pequenos de
, alcança valores
muito elevados e não realísticos. De fato, estas condensações acabam por separar-se do disco e se dissolvem.
Este fenômeno parece estar relacionado com o efeito ``hose'' (ver, e.g., Seção 1.2), já que este efeito é
favorecido para valores iniciais pequenos de ![]() e, portanto,
e, portanto, ![]() .
.
 |
 |
Por outro lado, valores para ![]() a partir de 350 pc já estabilizam o disco puro com relação a estas instabilidades locais (experimentos no(s). 13 e 14).
Entretanto, isto só é verdadeiro para os discos isotérmicos, que, com os parâmetros escolhidos nos experimentos 13
e 14, têm valores para
a partir de 350 pc já estabilizam o disco puro com relação a estas instabilidades locais (experimentos no(s). 13 e 14).
Entretanto, isto só é verdadeiro para os discos isotérmicos, que, com os parâmetros escolhidos nos experimentos 13
e 14, têm valores para ![]() maiores do que 1. O experimento no. 22 é idêntico ao 14, exceto pelo fato de que
tem um valor para
maiores do que 1. O experimento no. 22 é idêntico ao 14, exceto pelo fato de que
tem um valor para ![]() fixo em 0.5. Neste experimento, as instabilidades locais se manifestam novamente.
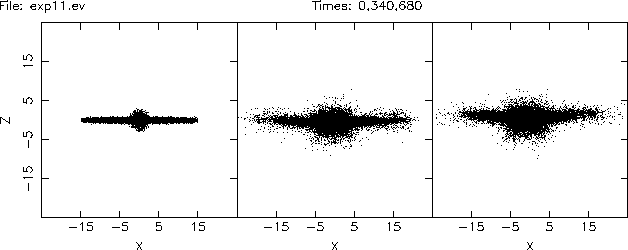
Verificamos também que a presença de um bojo estabiliza o disco com relação às instabilidades
locais, mesmo com escalas de altura tão pequenas quanto 200 pc (experimento no. 12), e mesmo sem a presença do
halo. Neste caso, porém, o disco ainda sofre de um efeito ``hose'' exacerbado, e a sua evolução o leva a um estado
em que a sua espessura atinge valores não realísticos (Fig. 3.3), além de ocorrerem distorções (``warps'') e
oscilações verticais no disco. Isto ocorre também nos experimentos 11 e 13, ou seja,
até
fixo em 0.5. Neste experimento, as instabilidades locais se manifestam novamente.
Verificamos também que a presença de um bojo estabiliza o disco com relação às instabilidades
locais, mesmo com escalas de altura tão pequenas quanto 200 pc (experimento no. 12), e mesmo sem a presença do
halo. Neste caso, porém, o disco ainda sofre de um efeito ``hose'' exacerbado, e a sua evolução o leva a um estado
em que a sua espessura atinge valores não realísticos (Fig. 3.3), além de ocorrerem distorções (``warps'') e
oscilações verticais no disco. Isto ocorre também nos experimentos 11 e 13, ou seja,
até ![]() pc e com ou sem bojo. Também é interessante que este efeito é expressivo, em geral,
apenas após mais de 1 Gano, e tanto mais rápido quanto mais instável o disco for, o que podemos avaliar pela sua
escala de altura e pela presença ou ausência do bojo.
Somente para
pc e com ou sem bojo. Também é interessante que este efeito é expressivo, em geral,
apenas após mais de 1 Gano, e tanto mais rápido quanto mais instável o disco for, o que podemos avaliar pela sua
escala de altura e pela presença ou ausência do bojo.
Somente para ![]() pc o disco puro é estável tanto às instabilidades
locais quanto a um efeito ``hose'' exagerado (experimento no. 14). Ao adicionarmos um halo nestes casos, porém
(experimentos 9 e 10), seu efeito estabilizador se manifesta, e o disco assume um comportamento mais realístico,
ou seja, sua estrutura vertical ganha importância durante sua evolução, mas ainda permanece fina como os
discos observados em galáxias vistas de perfil.
pc o disco puro é estável tanto às instabilidades
locais quanto a um efeito ``hose'' exagerado (experimento no. 14). Ao adicionarmos um halo nestes casos, porém
(experimentos 9 e 10), seu efeito estabilizador se manifesta, e o disco assume um comportamento mais realístico,
ou seja, sua estrutura vertical ganha importância durante sua evolução, mas ainda permanece fina como os
discos observados em galáxias vistas de perfil.
 |
É interessante, portanto, que a presença de um bojo adiciona estabilidade ao disco, e que isso se dá de forma ainda mais significativa com a presença do halo. Além disso, as variações na energia total e na posição do centro de massa durante as simulações tendem a diminuir com o aumento da estabilidade do disco.
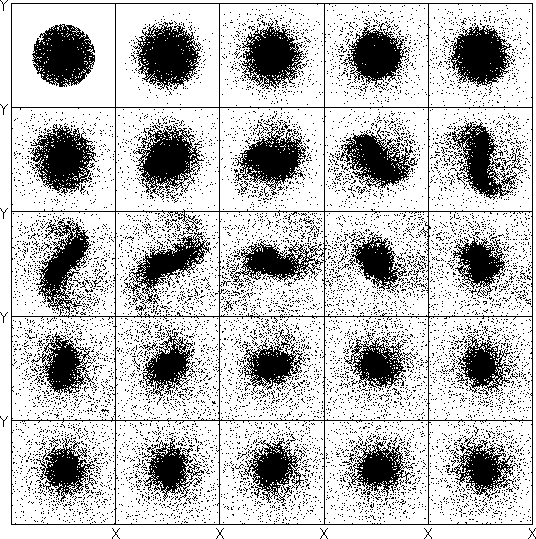
Vejamos qual é o comportamento dos sistemas simulados com relação à instabilidade de barra. Na Fig. 3.4, que se
refere ao experimento no. 14, vemos que um disco puro (exponencial e isotérmico)
é instável à formação de barra, conforme o esperado. A barra
se forma em cerca de ![]() anos e induz a formação de braços espirais proeminentes no conhecido
padrão ``grand design''. Este é um exemplo típico da formação de braços via barra. A barra se enfraquece
após cerca de
anos e induz a formação de braços espirais proeminentes no conhecido
padrão ``grand design''. Este é um exemplo típico da formação de braços via barra. A barra se enfraquece
após cerca de ![]() anos, mas ainda permanece por um período de tempo similar, dando lugar a
uma distorção oval, que persiste até o fim do experimento, em 2 Gano. Note que o período de rotação da barra
é substancialmente maior que o período orbital das estrelas, e que os braços desaparecem com o enfraquecimento
da barra. A Fig. 3.5 se refere ao mesmo experimento, porém exibe a evolução do sistema como seria visto de perfil.
Pode-se notar claramente o aquecimento vertical do disco, e como o enfraquecimento da barra dá origem a uma
estrutura similar a um bojo. Estes resultados corroboram aqueles divulgados por outros autores, e discutidos na
Seção 1.2.
anos, mas ainda permanece por um período de tempo similar, dando lugar a
uma distorção oval, que persiste até o fim do experimento, em 2 Gano. Note que o período de rotação da barra
é substancialmente maior que o período orbital das estrelas, e que os braços desaparecem com o enfraquecimento
da barra. A Fig. 3.5 se refere ao mesmo experimento, porém exibe a evolução do sistema como seria visto de perfil.
Pode-se notar claramente o aquecimento vertical do disco, e como o enfraquecimento da barra dá origem a uma
estrutura similar a um bojo. Estes resultados corroboram aqueles divulgados por outros autores, e discutidos na
Seção 1.2.
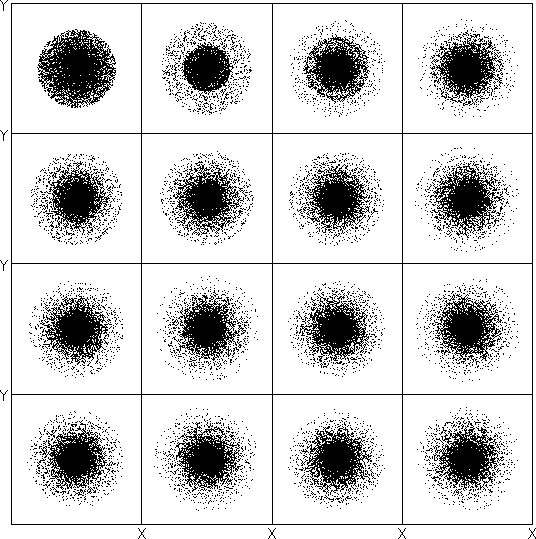
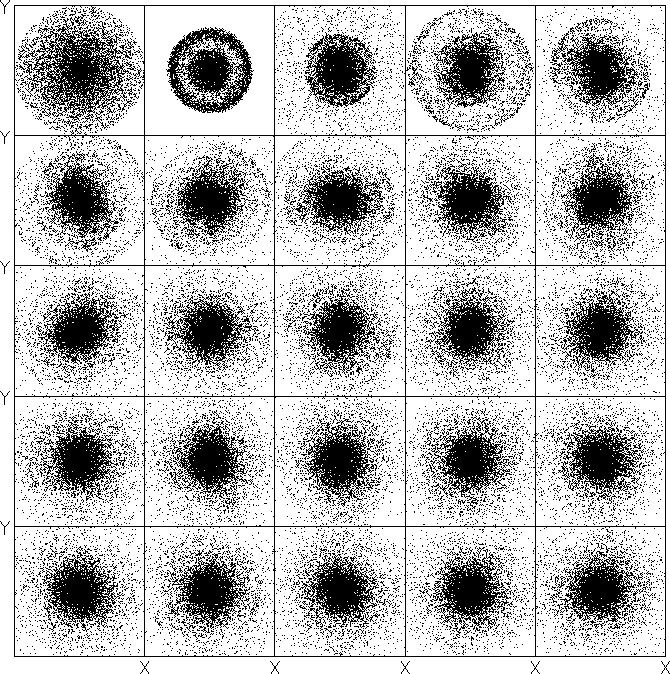
Entretanto, ao adicionarmos ao experimento bojo e halo, de forma a termos uma simulação mais realística, no sentido de reproduzir as características observadas em galáxias, nos encontramos face ao problema mais relevante enfrentado pelo mecanismo de instabilidade de barra: a dificuldade em formar uma barra em sistemas de disco que contêm uma alta concentração central de massa (ver Seção 1.2). As Fig(s). 3.6 e 3.7 mostram como se dá a evolução de um sistema completo (o experimento no. 9), que contém um disco que, isolado, é instável à formação da barra, de maneira similar ao exibido nas Fig(s). 3.4 e 3.5. Com a influência estabilizadora de bojo e halo, o disco torna-se estável e a barra não se desenvolve. Note que constatamos, através de experimentos como o de no. 11, que apenas a presença do bojo já é suficiente para inibir a formação de barra.
 |
Verificamos que, para incentivar a formação de uma barra em sistemas completos,
com bojo, disco e halo, podemos forçar um parâmetro
![]() de Toomre menor do que 1. No entanto, isto modifica as propriedades dinâmicas do disco, como discutido acima.
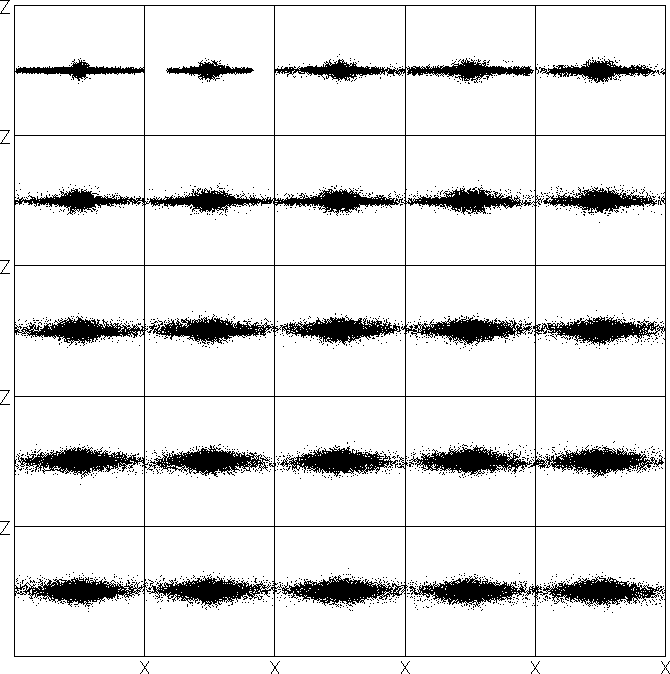
Na Fig(s). 3.8 e 3.9, exibimos a evolução do experimento no. 18, que é idêntico ao experimento no. 9 (exibido
nas Fig(s). 3.6 e 3.7), exceto pelo fato de que tem
de Toomre menor do que 1. No entanto, isto modifica as propriedades dinâmicas do disco, como discutido acima.
Na Fig(s). 3.8 e 3.9, exibimos a evolução do experimento no. 18, que é idêntico ao experimento no. 9 (exibido
nas Fig(s). 3.6 e 3.7), exceto pelo fato de que tem ![]() . Vemos que o sistema desenvolve uma barra que é,
porém, menor e menos excêntrica (portanto, mais fraca) que aquela que surge em discos puros e dá origem
ao padrão ``grand design''. De fato, neste experimento não vemos a formação conjunta de braços espirais.
A barra se forma em cerca de
. Vemos que o sistema desenvolve uma barra que é,
porém, menor e menos excêntrica (portanto, mais fraca) que aquela que surge em discos puros e dá origem
ao padrão ``grand design''. De fato, neste experimento não vemos a formação conjunta de braços espirais.
A barra se forma em cerca de
![]() anos, mais rapidamente que no disco puro; ela se enfraquece
gradual e lentamente, até a sua completa dissolução após cerca de 1.2 Gano. É interessante que, visto de perfil,
este sistema apresenta claramente a morfologia ``boxy-peanut''. Trataremos deste tema em detalhes mais adiante.
anos, mais rapidamente que no disco puro; ela se enfraquece
gradual e lentamente, até a sua completa dissolução após cerca de 1.2 Gano. É interessante que, visto de perfil,
este sistema apresenta claramente a morfologia ``boxy-peanut''. Trataremos deste tema em detalhes mais adiante.
 |
 |
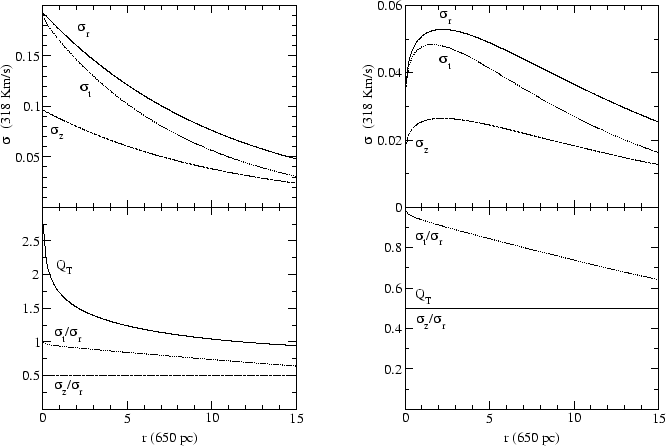
Na Fig. 3.10, podemos verificar quais são as modificações nas propriedades dinâmi-cas do disco ao forçarmos
um valor fixo para ![]() . Verificamos que a curva de rotação, a distribuição de massa, bem como
. Verificamos que a curva de rotação, a distribuição de massa, bem como ![]() e
e
![]() não se alteram. Evidentemente, a mudança mais brutal se refere à dispersão de velocidades. O
valor máximo para
não se alteram. Evidentemente, a mudança mais brutal se refere à dispersão de velocidades. O
valor máximo para ![]() , que é cerca de 60 Km/s no centro do disco isotérmico e com
, que é cerca de 60 Km/s no centro do disco isotérmico e com ![]() constante, cai para
cerca de 20 Km/s. O perfil radial da dispersão de velocidades também é alterado, e não tem mais o seu
valor máximo no centro. O perfil radial de
constante, cai para
cerca de 20 Km/s. O perfil radial da dispersão de velocidades também é alterado, e não tem mais o seu
valor máximo no centro. O perfil radial de ![]() também é alterado; por outro lado, as razões
também é alterado; por outro lado, as razões
![]() e
e
![]() permanecem as mesmas. Estas modificações fazem
com que a introdução de um valor fixo para
permanecem as mesmas. Estas modificações fazem
com que a introdução de um valor fixo para ![]() pareça não ser justificável, principalmente devido
ao valor excessivamente baixo para a dispersão de velocidades, que não é condizente com o observado.
Vimos na Seção 2.4 que o valor de
pareça não ser justificável, principalmente devido
ao valor excessivamente baixo para a dispersão de velocidades, que não é condizente com o observado.
Vimos na Seção 2.4 que o valor de ![]() na vizinhança solar é cerca de 30 Km/s. Para o disco
isotérmico e com
na vizinhança solar é cerca de 30 Km/s. Para o disco
isotérmico e com ![]() constante do experimento 9, o valor de
constante do experimento 9, o valor de ![]() é de 20 Km/s em cerca de
8 Kpc do centro. Porém, para o disco com
é de 20 Km/s em cerca de
8 Kpc do centro. Porém, para o disco com ![]() fixo do experimento 18, o valor de
fixo do experimento 18, o valor de ![]() é
de apenas cerca de 10 Km/s. Evidentemente, pode-se sugerir, por outro lado, que a dispersão
de velocidades nos discos de galáxias barradas é de fato substancialmente menor do que na
Galáxia. Isto poderia contornar o problema da formação de barras via a instabilidade de disco
em galáxias com baixas razões bojo/disco, porém não parece ser compatível com as observações
(ver Fig. 1.7) de que os valores para a dispersão de velocidades nos discos estão na ordem de
pelo menos 50 Km/s a cerca de 3 a 4 Kpc do centro.
é
de apenas cerca de 10 Km/s. Evidentemente, pode-se sugerir, por outro lado, que a dispersão
de velocidades nos discos de galáxias barradas é de fato substancialmente menor do que na
Galáxia. Isto poderia contornar o problema da formação de barras via a instabilidade de disco
em galáxias com baixas razões bojo/disco, porém não parece ser compatível com as observações
(ver Fig. 1.7) de que os valores para a dispersão de velocidades nos discos estão na ordem de
pelo menos 50 Km/s a cerca de 3 a 4 Kpc do centro.
Note que fixar um valor para ![]() menor do que 1 foi a única forma que encontramos para desenvolver uma
barra em sistemas com bojo e halo, mesmo para aqueles com bojos ainda menos proeminentes, que se referem
a galáxias com tipo morfológico Scd, mantendo o valor de 0.05 para o parâmetro de suavização
menor do que 1 foi a única forma que encontramos para desenvolver uma
barra em sistemas com bojo e halo, mesmo para aqueles com bojos ainda menos proeminentes, que se referem
a galáxias com tipo morfológico Scd, mantendo o valor de 0.05 para o parâmetro de suavização ![]() ,
seguindo os valores sugeridos por Merritt (1996; ver Seção 3.3.2).
De fato, para galáxias com bojos mais relevantes, nossos experimentos mostram que só é possível
formar uma barra se, além de fixar
,
seguindo os valores sugeridos por Merritt (1996; ver Seção 3.3.2).
De fato, para galáxias com bojos mais relevantes, nossos experimentos mostram que só é possível
formar uma barra se, além de fixar ![]() , aumentarmos o parâmetro de suavização para cerca de 0.25, o
que é significativamente maior do que o valor ótimo (ver Seção 3.3.2). O valor ótimo para
, aumentarmos o parâmetro de suavização para cerca de 0.25, o
que é significativamente maior do que o valor ótimo (ver Seção 3.3.2). O valor ótimo para
![]() de 0.05 nas simulações em que o utilizamos equivale a cerca de 30 pc. Para o desenvolvimento
de uma barra nas simulações de galáxias com bojos proeminentes (ver adiante), o valor de 0.25
para o parâmetro de suavização utilizado equivale a quase 1000 pc!
de 0.05 nas simulações em que o utilizamos equivale a cerca de 30 pc. Para o desenvolvimento
de uma barra nas simulações de galáxias com bojos proeminentes (ver adiante), o valor de 0.25
para o parâmetro de suavização utilizado equivale a quase 1000 pc!
 |
Apesar de todos estes problemas
é muito comum encontrarmos na literatura (Seção 1.2) experimentos que se utilizam destes artifícios
para a formação de barra em sistemas em que há, além do disco, uma componente esferoidal
(bojo e/ou halo). Sellwood & Moore (1999) realizam experimentos
em que ![]() (adequado ao valor de
(adequado ao valor de
![]() partículas utilizadas), e
partículas utilizadas), e ![]() . Nestes experimentos uma barra se desenvolve, porém isso se dá porque os
autores também simulam a queda de gás do halo no disco via o acréscimo gradual de partículas cinematicamente
frias. Combes & Sanders (1981) exibem o desenvolvimento de uma barra em um sistema completo. Porém, os
autores utilizam o método PM (ver Seção 3.3.1) com o tamanho das células cerca de 5 vezes maior do que
o sugerido pelas relações de Merritt (Eq(s). 3.52 e 3.53). Em Combes & Elmegreen (1993) o parâmetro de
suavização varia de 200 a 4000 pc, o que é muito superior ao sugerido para
. Nestes experimentos uma barra se desenvolve, porém isso se dá porque os
autores também simulam a queda de gás do halo no disco via o acréscimo gradual de partículas cinematicamente
frias. Combes & Sanders (1981) exibem o desenvolvimento de uma barra em um sistema completo. Porém, os
autores utilizam o método PM (ver Seção 3.3.1) com o tamanho das células cerca de 5 vezes maior do que
o sugerido pelas relações de Merritt (Eq(s). 3.52 e 3.53). Em Combes & Elmegreen (1993) o parâmetro de
suavização varia de 200 a 4000 pc, o que é muito superior ao sugerido para
![]() , o número de
partículas utilizado. Em Athanassoula & Sellwood (1986),
, o número de
partículas utilizado. Em Athanassoula & Sellwood (1986), ![]() , superior ao sugerido para as 40 mil
partículas dos experimentos. Athanassoula (1992a, b) realiza simulações em que a barra é estabelecida
a priori e
, superior ao sugerido para as 40 mil
partículas dos experimentos. Athanassoula (1992a, b) realiza simulações em que a barra é estabelecida
a priori e ![]() pc. Em Athanassoula & Misiriotis (2002) o valor de
pc. Em Athanassoula & Misiriotis (2002) o valor de ![]() é 0.0625, o que
é ainda elevado para o número alto de partículas utilizadas (
é 0.0625, o que
é ainda elevado para o número alto de partículas utilizadas (![]() ), e
), e ![]() é fixo em 0.9.
é fixo em 0.9.
Desta forma, parece que valores elevados para o parâmetro de suavização são uma condição
comumente adotada na literatura para a
formação de barras, via o cenário vigente de instabilidade no disco, em sistemas realísticos com bojos
proeminentes. Porém, não é claro até que ponto estes valores tão elevados
são justificáveis do ponto de vista físico, face à suavização forçada em escalas de tamanho tão grandes.
Nas Fig(s). 3.11 e 3.12 exibimos a evolução de um sistema completo que simula uma galáxia lenticular. A
única forma que encontramos para que este sistema (e outros com bojos proeminentes)
desenvolva uma barra foi fixar ![]() em 0.25 e utilizar
em 0.25 e utilizar ![]() , o que equivale a aproximadamente 1 Kpc
(experimento no. 34). Assim, para
formar uma barra em uma galáxia de tipo morfológico recente (S0-Sa) é preciso forças significativamente
distintas da Newtoniana e, além disso, é preciso que os discos sejam cinematicamente frios. Enquanto
a primeira condição não parece ser justificável, a segunda certamente contraria as observações.
Este é, de fato, o principal entrave atual para o cenário vigente de formação de barras em galáxias
(ver Seção 1.2).
, o que equivale a aproximadamente 1 Kpc
(experimento no. 34). Assim, para
formar uma barra em uma galáxia de tipo morfológico recente (S0-Sa) é preciso forças significativamente
distintas da Newtoniana e, além disso, é preciso que os discos sejam cinematicamente frios. Enquanto
a primeira condição não parece ser justificável, a segunda certamente contraria as observações.
Este é, de fato, o principal entrave atual para o cenário vigente de formação de barras em galáxias
(ver Seção 1.2).
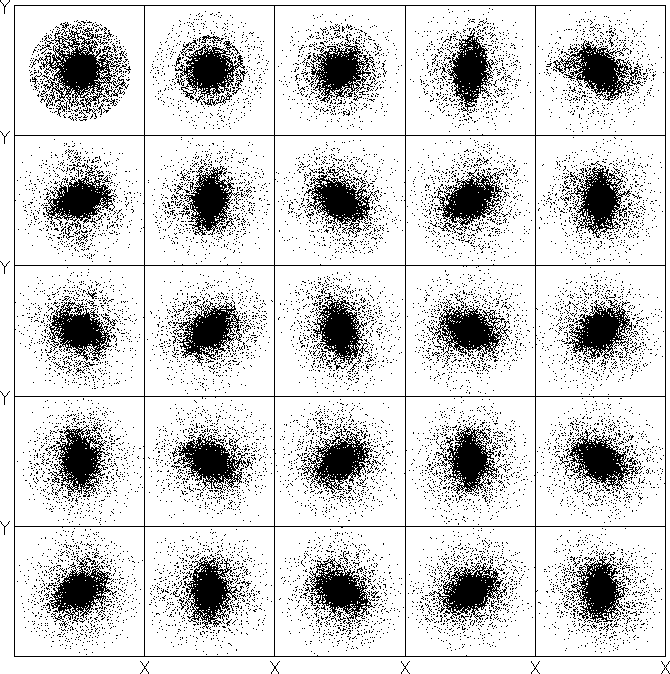 |
No experimento das Fig(s). 3.11 e 3.12 nota-se que a barra se forma em cerca de ![]() anos e é perene.
É interessante notar que o resultado desta simulação é semelhante às lenticulares barradas observadas
(e.g., NGC 4665; ver Apêndice A).
anos e é perene.
É interessante notar que o resultado desta simulação é semelhante às lenticulares barradas observadas
(e.g., NGC 4665; ver Apêndice A).
Alguns resultados que encontramos também corroboram outros já na literatura (ver Seção 1.2).
Em todos os experimentos em que houve a formação de uma barra isto se dá de forma rápida, sempre em um intervalo
de tempo da ordem de algumas vezes 10![]() anos, compatível com o cenário de instabilidade global
em discos. Isto foi independente de qualquer outro parâmetro ou condição
inicial. Por outro lado, verificamos que, em geral, uma vez formadas, as barras se mantêm por uma fração
maior da evolução do sistema se o bojo é mais proeminente. Em alguns casos a barra persiste por mais de 2 Gano.
Isto pode ser apenas um resultado de que para
o desenvolvimento de uma barra nestes sistemas foi necessário o uso dos artifícios que discutimos acima, e
que tornam o disco mais instável. Por outro lado, Athanassoula (2003) sugere, através de um estudo analítico,
que quanto mais importante for a componente esferoidal em uma galáxia barrada, maior é a troca
de momento angular entre a barra e o halo, o que acaba por reforçar a barra (ver também Seção 1.2).
anos, compatível com o cenário de instabilidade global
em discos. Isto foi independente de qualquer outro parâmetro ou condição
inicial. Por outro lado, verificamos que, em geral, uma vez formadas, as barras se mantêm por uma fração
maior da evolução do sistema se o bojo é mais proeminente. Em alguns casos a barra persiste por mais de 2 Gano.
Isto pode ser apenas um resultado de que para
o desenvolvimento de uma barra nestes sistemas foi necessário o uso dos artifícios que discutimos acima, e
que tornam o disco mais instável. Por outro lado, Athanassoula (2003) sugere, através de um estudo analítico,
que quanto mais importante for a componente esferoidal em uma galáxia barrada, maior é a troca
de momento angular entre a barra e o halo, o que acaba por reforçar a barra (ver também Seção 1.2).
Nós estimamos a velocidade de rotação do padrão das barras ![]() , em nossas simulações, em
cerca de 30 Km s
, em nossas simulações, em
cerca de 30 Km s![]() Kpc
Kpc![]() . Em geral,
. Em geral, ![]() cai ligeiramente durante a evolução dos
experimentos. Não verificamos uma variação sistemática na rotação de barras em sistemas que representam
galáxias de tipos morfológicos distintos. Resultados semelhantes foram encontrados por Combes & Elmegreen
(1993). Porém, as observações indicam que
cai ligeiramente durante a evolução dos
experimentos. Não verificamos uma variação sistemática na rotação de barras em sistemas que representam
galáxias de tipos morfológicos distintos. Resultados semelhantes foram encontrados por Combes & Elmegreen
(1993). Porém, as observações indicam que
![]() Km s
Km s![]() Kpc
Kpc![]() , embora
haja um largo espalhamento em torno deste valor médio, e estas medidas observacionais sofrem de
grandes incertezas (Seção 1.2). O comprimento das barras também foi estimado nas simulações.
Mais uma vez em acordo com as observações (ver Capítulo 4), este valor variou entre 4 a 8 Kpc.
, embora
haja um largo espalhamento em torno deste valor médio, e estas medidas observacionais sofrem de
grandes incertezas (Seção 1.2). O comprimento das barras também foi estimado nas simulações.
Mais uma vez em acordo com as observações (ver Capítulo 4), este valor variou entre 4 a 8 Kpc.
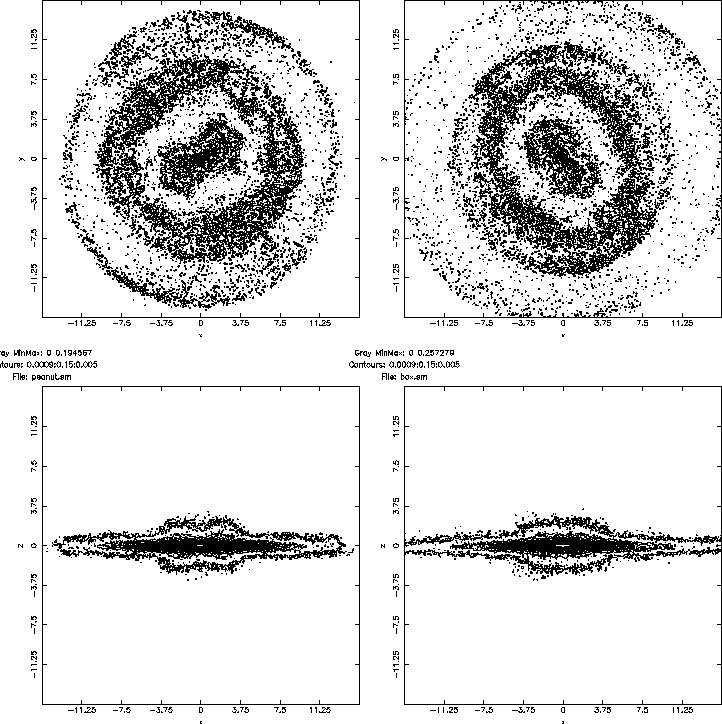 |
Vejamos agora que informações podemos extrair das simulações realizadas, que dizem respeito ao espessamento
vertical da barra. Nas Fig(s). 3.9 e 3.5 já ficou evidente que ocorre um aquecimento vertical gradual do disco e
que, na região da barra, este aquecimento é mais vigoroso, o que produz uma estrutura que nos remete a um bojo,
algumas vezes com a morfologia ``boxy-peanut''. Na Fig. 3.13 mostramos em maiores detalhes o surgimento desta
morfologia de certa forma peculiar. Note que a componente bojo do sistema foi eliminada nesta figura com o intuito
de realçar a forma ``boxy-peanut''. Isto também indica que, de fato, esta morfologia é uma estrutura inerente à
barra e somente a ela. No momento que esta estrutura está presente, a barra deixa de fazer parte do disco,
assumindo uma estrutura vertical mais proeminente através do aumento do valor de ![]() . As estrelas que
compõem esta estrutura já deixaram de fazer parte do disco, cuja componente vertical
permanece ainda relativamente fina. É interessante notar que a morfologia ``peanut'' se apresenta quando a barra é vista
de perfil e através de uma linha de visada perpendicular a ela, enquanto que a morfologia ``boxy'' fica evidente
quando a barra é vista também de perfil, mas através de uma linha de visada paralela a ela.
Estas morfologias foram identificadas nos nossos experimentos, tanto naqueles que representam galáxias de tipo
morfológico tardio quanto naqueles representativos de galáxias com tipo morfológico recente. No entanto, em
uma galáxia real, na qual não podemos eliminar o bojo, estas morfologias devem ficar menos evidentes se o bojo
for proeminente. Em nossas simulações, a morfologia ``boxy-peanut'' tende a se dissolver após cerca de
1 Gano, o que pode, portanto, ser um indício observacional para a identificação de barras recém-formadas.
. As estrelas que
compõem esta estrutura já deixaram de fazer parte do disco, cuja componente vertical
permanece ainda relativamente fina. É interessante notar que a morfologia ``peanut'' se apresenta quando a barra é vista
de perfil e através de uma linha de visada perpendicular a ela, enquanto que a morfologia ``boxy'' fica evidente
quando a barra é vista também de perfil, mas através de uma linha de visada paralela a ela.
Estas morfologias foram identificadas nos nossos experimentos, tanto naqueles que representam galáxias de tipo
morfológico tardio quanto naqueles representativos de galáxias com tipo morfológico recente. No entanto, em
uma galáxia real, na qual não podemos eliminar o bojo, estas morfologias devem ficar menos evidentes se o bojo
for proeminente. Em nossas simulações, a morfologia ``boxy-peanut'' tende a se dissolver após cerca de
1 Gano, o que pode, portanto, ser um indício observacional para a identificação de barras recém-formadas.
Veja que a morfologia ``boxy-peanut'' se desenvolve em escalas de tempo da ordem da escala de tempo dinâmica do
sistema, ou seja, após a formação da barra, em poucas rotações a galáxia desenvolve esta morfologia. A barra
começa a ganhar uma estrutura vertical importante muito rapidamente. Porém, o valor de ![]() ainda é baixo
se comparado com aqueles que obtivemos no Capítulo 2. De fato, nossos experimentos mostram que ocorre um aumento
gradual no valor de
ainda é baixo
se comparado com aqueles que obtivemos no Capítulo 2. De fato, nossos experimentos mostram que ocorre um aumento
gradual no valor de ![]() na barra, mas que, no entanto, mesmo após 2 Gano,
na barra, mas que, no entanto, mesmo após 2 Gano, ![]() raramente ultrapassou
50 Km/s. Assim, podemos concluir que o mecanismo que produz a estrutura ``boxy-peanut'' é rápido e, qualquer
que seja o mecanismo responsável pelo espessamento da barra que observamos no Capítulo 2, este deve ser
lento e gradual. Este resultado é compatível com o cenário que estamos sugerindo, no qual o espessamento
da barra é provocado pelo mecanismo Spitzer-Schwarzchild de aquecimento gradual do disco
(Seção 2.4); e também é compatível com
o resultado que apresentaremos no Capítulo 4, que sugere que a diferença de idade entre barras finas
(portanto jovens) e espessas (portanto evoluídas) é substancialmente superior a 1 Gano. Além disso, o
fato de a estrutura ``boxy-peanut'' se desenvolver rapidamente pode estar indicando que são processos
que envolvem as ressonâncias verticais, e/ou o efeito ``hose'', os responsáveis por esta estrutura. No
entanto, estes processos podem cessar quando o valor de
raramente ultrapassou
50 Km/s. Assim, podemos concluir que o mecanismo que produz a estrutura ``boxy-peanut'' é rápido e, qualquer
que seja o mecanismo responsável pelo espessamento da barra que observamos no Capítulo 2, este deve ser
lento e gradual. Este resultado é compatível com o cenário que estamos sugerindo, no qual o espessamento
da barra é provocado pelo mecanismo Spitzer-Schwarzchild de aquecimento gradual do disco
(Seção 2.4); e também é compatível com
o resultado que apresentaremos no Capítulo 4, que sugere que a diferença de idade entre barras finas
(portanto jovens) e espessas (portanto evoluídas) é substancialmente superior a 1 Gano. Além disso, o
fato de a estrutura ``boxy-peanut'' se desenvolver rapidamente pode estar indicando que são processos
que envolvem as ressonâncias verticais, e/ou o efeito ``hose'', os responsáveis por esta estrutura. No
entanto, estes processos podem cessar quando o valor de ![]() ainda é relativamente baixo, e o
mecanismo Spitzer-Schwarzchild pode então estar causando a maior parte do aumento em
ainda é relativamente baixo, e o
mecanismo Spitzer-Schwarzchild pode então estar causando a maior parte do aumento em ![]() e
do espessamento vertical da barra.
e
do espessamento vertical da barra.